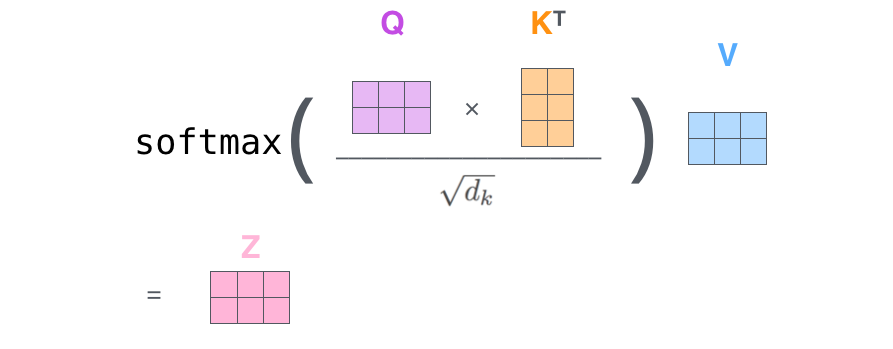Transformer 2025-01-29

本文发表于 340 天前，其中的信息可能已经事过境迁

文章摘要 FakeGPT

加载中...|

此内容根据文章生成，并经过人工审核，仅用于文章内容的解释与总结投诉

1 引言

现有的大模型，大部分都是decode-only结构。attention is all you need太过精炼，很多信息都被一笔带过了。所以学习过程中难免能产生一些疑问。比如什么是decode-only，大模型都是基于注意力机制的，什么是注意力机制，其中的QKV又怎么理解？

本文旨在通过解决学习过程中的一些疑问，将知识点串起来，从而尽可能用说人话的方式，说明transformer中的Q和K。

2 前置知识

在我们深入展开QKV之前，有几个知识点是需要知道的，如果不知道，等看到对应的地方跳回来看也行。

2.1 dot product的现实意义

两个向量相乘，实际上是算算他们的点积。

点积的公式：

| a | | b | c o s θ

其中 $a 、 b$ 是向量， $θ$ 是两个向量的夹角。当两个向量方向越接近(越相似),cosθ越接近1,点积值越大，当两个向量垂直时,cosθ=0,点积为0，当两个向量方向相反时,cosθ=-1,点积为负。

所以如果我们有两个向量，他们的点积越大，可以表示他们在特定的空间中夹角更小，也就是向量靠的更近。在语义空间中，如果是两个词，那他们就更相似、更有关系

2.2 反向传播和Loss函数

损失函数是衡量模型预测输出与真实标签之间差异的数学度量，而反向传播是一种基于链式法则的梯度计算算法，用于计算损失函数对网络中每个参数的偏导数，从而指导参数的优化更新，使损失函数逐步最小化。

2.3 transformer multihead attention的代码实现

python

class MultiHeadAttention(nn.Module):

    def __init__(self, d_in, d_out, context_length, dropout, num_heads, qkv_bias=False):
        super().__init__()
        assert d_out % num_heads == 0, "d_out must be divisible by num_heads"
        self.d_out = d_out
        self.num_heads = num_heads
        self.head_dim = d_out // num_heads  
        self.W_query = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.W_key = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.W_value = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.out_proj = nn.Linear(d_out, d_out) 
        self.dropout = nn.Dropout(dropout)
        self.register_buffer("mask", torch.triu(torch.ones(context_length, context_length), diagonal=1))


    def forward(self, x):
        b, num_tokens, d_in = x.shape
        keys = self.W_key(x)  # Shape: (b, num_tokens, d_out)
        queries = self.W_query(x)
        values = self.W_value(x)
        keys = keys.view(b, num_tokens, self.num_heads, self.head_dim)
        values = values.view(b, num_tokens, self.num_heads, self.head_dim)
        queries = queries.view(b, num_tokens, self.num_heads, self.head_dim)
        keys = keys.transpose(1, 2)
        queries = queries.transpose(1, 2)
        values = values.transpose(1, 2)
        attn_scores = queries @ keys.transpose(2, 3)  
        mask_bool = self.mask.bool()[:num_tokens, :num_tokens]
        attn_scores.masked_fill_(mask_bool, -torch.inf)
        attn_weights = torch.softmax(attn_scores / keys.shape[-1]**0.5, dim=-1)
        attn_weights = self.dropout(attn_weights)
        context_vec = (attn_weights @ values).transpose(1, 2)
        context_vec = context_vec.contiguous().view(b, num_tokens, self.d_out)
        context_vec = self.out_proj(context_vec) 
        return context_vec

3 正文开始：注意力机制

3.1 tarnsformer的流程

整个transformer流程（不考虑multi-head的情况）： image.png

文本输入 → 词嵌入（Embedding）得到 E。
E + 位置编码（Positional Encoding） → 得到 X（含位置信息）。
X 通过可学习的 Wq, Wk, Wv 生成 Q, K, V。
计算缩放点积注意力：

A t t e n t i o n (Q, K, V) = s o f t m a x (Q K^{T} / \sqrt{d_{k}}) V

3.2 注意力公式

注意力机制是transformer的核心。我们从其公式入手，我们一步步反推，就跟爬虫逆向跟堆栈一样，如果不知道这个问题的答案就向上找概念和定义，直到找到最初的最小化的定义。

A t t e n t i o n (Q, K, V) = s o f t m a x (Q K^{T} / \sqrt{d_{k}}) V

$\sqrt{d_{k}}$ 是缩放因子
$s o f t m a x$ 是函数

这里我们可以先解释 $\sqrt{d_{k}}$ ，代表的是 $Q$ 和 $K$ 的维度。目的是如果 $Q K^{T}$ 的结果非常大，那么经过 $s o f t m a x$ 之后就会非常接近1，而其他的值就会接近0。这种现象我们称为梯度消失

现在我们回到 $Q 、 K 、 V$

image.png

大部分的blog和视频材料会说

Q是查询
K是键
V是值

第一次看到这个概念的时候，我真是无奈了，典型的不说人话。通过凝练和比喻，让我不得不问出

QUESTION

到底什么是Q、K、V？

3.2.1 Q、K矩阵

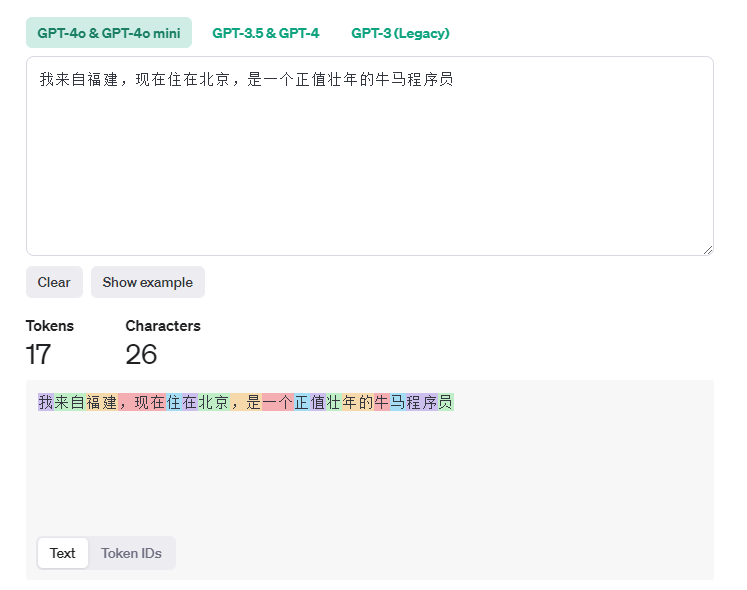
比如我们有这么一句话：

我来自福州，现在住在北京，是一个正值壮年的牛马程序员

image.png

我们把这个句子拆解以后，比如程序个词，我们从语义上理解，他应该是和员连在一起的。但是机器不知道，所以它为了知道其他词的关系，会对员发出询问，这个询问是Q矩阵中的一个向量，我们称为 $Q_{i}$ 。

程序：“员，我和你有啥关系啊？” 员：“我是你的后缀啊”

但是又注意到了，程序不止要问员，他还会问别的token，或者说，它会对每一个token都会发出询问（Query）。比如他会问

“牛，你是个形容我的词么？” “马，你是我的坐骑么？” “北京，你和我是什么关系”

而每一个token会把自己的回答（注意，实际上回答的是特征，而不是直接的答案）放在K矩阵中，K矩阵中的每一个向量 $K_{i}$ ，都是对Q矩阵中 $Q_{i}$ 的回答。

但是随之而来的问题就是

QUERTION

为什么这么问？
这么问准确么？
问错了怎么办？

先粗暴给出答案：

随便问的
就是不准
问错了也没事，因为模型会通过反向传播不断地学习正确的方式，从而修正它

更准确的说，是会修正Q、K、V的来源， $W_{q}$ 、 $W_{k}$ 、 $W_{v}$ 。所以我们先要理解这个三个 $W_{q}$ 、 $W_{k}$ 、 $W_{v}$

QUESTION

什么是 $W_{q}$ 、 $W_{k}$ 、 $W_{v}$ ？

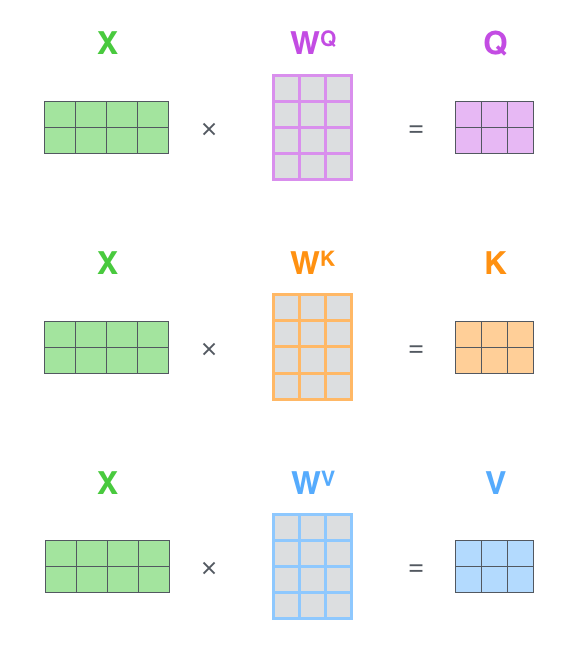
3.3 权重矩阵 $W_{q}$ 、 $W_{k}$ 、 $W_{v}$

$Q 、 K 、 V$ 是通过三个矩阵 $W_{q}$ 、 $W_{k}$ 、 $W_{v}$ 和embedding过的输入 $X$ ，相乘得来。而 $W_{q}$ 、 $W_{k}$ 、 $W_{v}$ 它在生成的初期，是随机的。

Q = W_{q} X

K = W_{k} X

V = W_{v} X

image.png

我们看一段多头注意力的代码，在注意力这个部分，直接就使用了一个transformer中的线性层，而这个线性层只规定了大小，其内容是完全随机的。

python

class MultiHeadAttention(nn.Module):

    def __init__(self, d_in, d_out, context_length, dropout, num_heads, qkv_bias=False):
        super().__init__()
        assert d_out % num_heads == 0, "d_out must be divisible by num_heads"
        self.d_out = d_out
        self.num_heads = num_heads
        self.head_dim = d_out // num_heads


		# ！！！！！！！关注这里三个矩阵在这里初始化
        self.W_query = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.W_key = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.W_value = nn.Linear(d_in, d_out, bias=qkv_bias)
		# ！！！！！！！初始化结束



        self.out_proj = nn.Linear(d_out, d_out)
        self.dropout = nn.Dropout(dropout)
        self.register_buffer("mask", torch.triu(torch.ones(context_length, context_length), diagonal=1))

3.3.1 形象化的例子： $W_{q}$ 、 $W_{k}$ 、 $W_{v}$ 的三个阶段，给与Q、K、V的影响

训练初期：当 $W_{q}$ 、 $W_{k}$ 、 $W_{v}$ 刚刚被随机初始化

随机的Wq会让Q矩阵乱问，Wk也让K矩阵乱回。

程序 -> 员：“阿巴阿巴阿巴阿巴” 员 -> 程序：“helw123928130啊冷冻机房”

然后这一轮结束，我们通过损失函数，发现这也太牛头不对马嘴了，下一轮调整一下吧

训练中期：初步学习语法特征

Wq和Wk已经学习到了语法特征，此刻Q和K可以让输入内容获取相对准确的表示。然后这一轮结束，感觉有点对了。

程序 -> 员：“我和你是不是有什么关系？” 员 -> 程序：“我表达的是某个词的后缀，但是我不知道我和你是不是有关系”

训练后期：已收敛

Wq和Wk已经学习到精细化的语义特征，所以Q和K可以更准确的表示特征查询和特征关系

程序 -> 员：“我是个名词，我需要确定我是否有修饰词和词缀，来完整我的语义，你是否是我的词缀？” 员 -> 程序：“我是单个词缀，我需要和其他内容结合，我和你可以组成程序员。”

4 还有几个问题

QUESTION

为什么需要权重矩阵，而不能直接随机出QKV，然后我们直接调整QKV？
为什么是三个？
我都知道他们是什么了，为什么 $Q K^{T}$ 表示注意力？

4.1.1 为什么需要权重矩阵，而不能直接随机出QKV？

如果我们直接通过训练修改Q、K、V，那么任意输入都没有机会参与注意力的计算，因为Q、K、V直接给出来，那么任意输入的注意力就都是一样的。（你觉得河里么）

4.1.2 为什么是三个？

其实这有好几个衍生问题：

Wq、Wk和Wv既然是随机初始化的，为什么他们能被赋予我们说的现实意义，也就是说为什么随机的权重矩阵经过学习和X相乘之后，能表示动态特征查询器和特征关系编码器以及语义信息本体
如果我增加为四个或者五个呢？

要回答为什么是三个，首先回答，Q、K的含义。贯穿了全文，Q、K都是说是Query和Key或者动态特征查询器和特征关系编码器。但是，这意义其实是人为赋予的。也就是说，既然Q和K一通计算了两个词在空间中的相似度，且意义是人为赋予的，那么Q和K的概念其实可以转换。因为我们需要Q和K共同去计算词的相似度。

那么接下来说为什么是三个，如果我们如果增加了一个M矩阵，会怎样？

计算的复杂度增加了。
Q、K、M（假设我们增加的）的概念是有重叠

这两者就造成了收益的递减。

同时，即使是Q和K，两者也不是绝对正交的。因为他们本质上都是一个输入空间的不同投影。也就是即使通过训练，这两者才概念上也被人为的划分了，对于神经网络而言，它只是寻找最优的特征表示，而不是严格的角色分工。所以Q和K依然存在意义的重叠。所以理论上，模型不是完美的。

4.1.3 $Q K^{T}$ 为什么表示注意力？

$Q$ 和$K^T是进行点积，在[[Transformer中的Q和K 2025-01-29#2 前置知识#2.1 dot product的现实意义]]前置知识部分，我们已经说过：

点积越大，就说明他们之间的夹角 $θ$ 之间越小，也就是他们越靠近，他们关联越大。

5 总结

所以 $W_{q}$ 、 $W_{k}$ 、 $W_{v}$ ，经过反复的总结和提炼，最终浓缩成这段：

$W_{q}$ 、 $W_{k}$ 、 $W_{v}$ 是三个独立的可学习矩阵，分别负责将输入映射到三个独立的特征空间。当输入序列经过词嵌入得到 $X$ 后，通过矩阵乘法
$Q = W q \cdot X$ → 生成动态特征查询器
$K = W k \cdot X$ → 构建特征关系编码器
$V = W v \cdot X$ → 保留语义信息本体
在训练过程中，通过反向传播，三个矩阵获得差异化的优化信号：
$W q$ 的梯度主要优化跨元素关系建模能力
$W k$ 的梯度重点增强特征区分度
$W v$ 的梯度稳定调整信息保留策略
$Q 、 K$ 在的意义是人为赋予的，我们最终需要的是 $Q K^{T}$ ，表示了每个词与其他词的关联度（注意力）。
通过 $\sqrt{d_{k}}$ ，进行缩放，防止梯度消失
经过 $s o f t m a x$ 将分数转为概率分布
最后与V相乘得到得到加权后的特征

更说人话一点，先前我们已经知道了attention其实是一个关于 $Q 、 K 、 V$ 的公式。所以我们可以说transformer的注意力来自 $Q 、 K 、 V$ 三个矩阵，而 $Q 、 K 、 V$ 又是 $W q X ， W k X ， W v X$ 得来的。 $X$ 是词嵌入的向量， $W q 、 W k 、 W v$ 是训练（反向传播）学习大量语料，抽象地表示了注意力的模式，是我们调整和训练的核心之一。所以当它乘以X的时候，我们就得到了 $Q 、 K 、 V$ ，也就可以通过之前的公式计算出当前输入的注意力分布。（再结合这张图体会体会）

image.png

6 参考

[1] PP鲁. "注意力机制到底在做什么,Q/K/V怎么来的?一文读懂Attention注意力机制". 知乎, 2023. https://www.zhihu.com/tardis/zm/art/414084879

[2] Alammar, J. "The Illustrated Transformer". Jay Alammar - Visualizing Machine Learning One Concept at a Time, 2018. https://jalammar.github.io/illustrated-transformer/

[3] 3Blue1Brown. "【官方双语】GPT是什么?直观解释Transformer | 深度学习第5章". 哔哩哔哩, 2024. https://www.bilibili.com/video/BV13z421U7cs/

[4] 3Blue1Brown. "【官方双语】直观解释注意力机制，Transformer的核心 | 【深度学习第6章】". 哔哩哔哩, 2024. https://www.bilibili.com/video/BV1TZ421j7Ke/

[5] 王木头学科学. "损失函数是如何设计出来的?直观理解最小二乘法和极大似然估计法". 哔哩哔哩, 2021. https://www.bilibili.com/video/BV1Y64y1Q7hi/

[6] Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., & Polosukhin, I. (2017). Attention is all you need. arXiv preprint arXiv:1706.03762.[1706.03762] Attention Is All You Need

Transformer 2025-01-29

作者phimes

发布于2025/1/29

更新于今日内

许可协议 CC BY-NC-SA 4.0

署名-非商业性使用-相同方式共享 4.0 国际

算法原理

反馈与投诉

Transformer 2025-01-29

1 引言 ​

2 前置知识 ​

2.1 dot product的现实意义 ​

2.2 反向传播和Loss函数 ​

2.3 transformer multihead attention的代码实现 ​

3 正文开始：注意力机制 ​

3.1 tarnsformer的流程 ​

3.2 注意力公式 ​

3.2.1 Q、K矩阵 ​

3.3 权重矩阵Wq、Wk、Wv ​

3.3.1 形象化的例子：Wq、Wk、Wv的三个阶段，给与Q、K、V的影响 ​

4 还有几个问题 ​

4.1.1 为什么需要权重矩阵，而不能直接随机出QKV？ ​

4.1.2 为什么是三个？ ​

4.1.3 QKT为什么表示注意力？ ​

5 总结 ​

6 参考 ​

1 引言

2 前置知识

2.1 dot product的现实意义

2.2 反向传播和Loss函数

2.3 transformer multihead attention的代码实现

3 正文开始：注意力机制

3.1 tarnsformer的流程

3.2 注意力公式

3.2.1 Q、K矩阵

3.3 权重矩阵 $W_{q}$ 、 $W_{k}$ 、 $W_{v}$

3.3.1 形象化的例子： $W_{q}$ 、 $W_{k}$ 、 $W_{v}$ 的三个阶段，给与Q、K、V的影响

4 还有几个问题

4.1.1 为什么需要权重矩阵，而不能直接随机出QKV？

4.1.2 为什么是三个？

4.1.3 $Q K^{T}$ 为什么表示注意力？

5 总结

6 参考