前馈神经网络（FFN）详解（二）：从激活函数到MOE

本文发表于 216 天前，其中的信息可能已经事过境迁

1 前言

时隔两周未更新，未曾预料此文篇幅如此之长，其间反复推敲修改多次。主要是不想让读者死背结论，而是希望能切实地从最初的设计理念出发，沿着优化过程中涌现的关键问题，来审视近年来激活函数以及大模型中FFN结构的演变。

因为激活函数处在一种微妙的境地：表面看，如 ReLU 般形态简单、计算高效，其设计意图一目了然；但深究起来，却隐藏着复杂的优化空间。这种由浅入深的过程颇具挑战性，因为它要求我们同时具备数学推导的微观能力和架构理解的宏观视野。因此，我将从优化面临的实际问题出发，以问题为导向，系统梳理不同激活函数的特性与局限，以此视角揭示模型结构变迁的深层原因。

2 优化激活函数思路

2.1 优化目标：

激活函数优化目标有很多，其中训练稳定性、计算效率和任务适应性是当前研究较多的方向。

2.1.1 训练稳定性

训练稳定性本身又可以从三个方面来看，一个是激活函数的导数特性，一个是零均值输出，还有就是激活函数的饱和性。

激活函数的导数特性：
- 梯度消失：如果激活函数在其大部分定义域内导数都非常小，例如Sigmoid和Tanh函数在其饱和区域，那么在深层网络中，这些小导数的连乘会导致梯度迅速减小，使得浅层网络的参数难以更新。
- 梯度爆炸：虽然不完全由激活函数本身决定，但如果激活函数的导数值持续大于1，并且网络权重较大，也可能促使梯度在反向传播中指数级增大。
- 零梯度区域：像ReLU函数在输入为负时导数为零，可能导致“神经元死亡”问题，即一旦神经元进入失活状态，就无法再通过梯度下降进行恢复，从而影响网络的有效容量和稳定性。
激活函数输出值的分布特性，特别是均值：
- 零均值输出 (Zero-centered Output)：如果激活函数的输出均值不接近零（例如Sigmoid的输出范围是(0,1)，ReLU的输出范围是[0, ∞)，可能会导致后续层权重的梯度在更新时方向受限。具体来说，所有梯度分量可能倾向于同时为正或同时为负，使得优化路径呈现低效的“之字形”，减慢收敛速度，并可能影响训练的最终稳定性。输出接近零均值的激活函数比如Tanh和ELU或配合使用归一化层如Batch Normalization，它会调整输入的均值，有助于缓解此问题。
激活函数的饱和性 ：
- 饱和区域：指激活函数进入梯度接近于零的区域。双侧饱和的激活函数（如Sigmoid和Tanh）在其输入绝对值较大时容易饱和。单侧饱和的激活函数（如ReLU，在负区域饱和）也存在类似问题。当神经元大部分时间工作在饱和区域时，梯度信息丢失，学习过程停滞，影响稳定性。理想情况下，激活函数应尽可能减少神经元进入饱和状态的概率，或者像ReLU一样至少在一侧保持非饱和。

2.1.2 计算效率

复杂的数学运算会显著增加前向传播和反向传播的计算开销，特别是在大规模模型部署场景中。因此，激活函数设计倾向于在数学简洁性与性能表现之间寻求平衡。一般来说，我们关注三个部分。

激活函数本身的数学形式直接决定了其计算开销。例如，ReLU函数 (max(0, x)) 仅涉及一次比较操作，计算极其高效。相比之下，Sigmoid (1 / (1 + exp(-x))) 和 Tanh ((exp(x) - exp(-x)) / (exp(x) + exp(-x))) 函数涉及指数运算，其计算成本相对较高。尽管现代计算库和硬件（如GPU、TPU）对这些运算进行了优化，但在计算资源受限或需要极低延迟的场景下，这种差异仍然显著。
反向传播算法依赖于激活函数导数的计算。理想情况下，激活函数的导数形式应同样简洁。
硬件亲和性与优化一些看似复杂的函数，如果能够被硬件或底层库高度优化，其实际开销可能低于预期。

2.1.3 任务适应性

适应性方面不同网络架构对激活函数的需求存在显著差异，在自然语言处理及更广泛的序列建模任务中，GELU (Gaussian Error Linear Unit) 和Swish/SiLU (Sigmoid-weighted Linear Unit) 等平滑且非单调的激活函数，在Transformer模型中通常能取得优于ReLU的性能。而对于卷积神经网络主导的视觉任务，如图像分类或目标检测，ReLU因其“非黑即白”的稀疏激活特性仍是常见选择。这种硬阈值行为类似快速的特征筛选机制，能高效提取图像中的局部结构比如边缘、纹理，符合视觉任务对明确空间关系的偏好。

举个例子来说，当有人说“尊贵的X1车主“的时候，如果不了解上下文，人们很难判断这是在阴阳怪气还是正面情绪。但是GELU/Swish的“部分激活”特性符合这种情况：

"恭喜尊贵的X1车主提车成功"语境下，"尊贵"可能激活0.8的正面程度
"又是尊贵的X1车主，真是让人羡慕"的阴阳怪气语境下，可能只激活0.2的正面程度
"尊贵的X1车主请注意，您的车贷还款日到了"的中性语境下，可能激活0.5

2.2 优化方向

主流的优化的方向可以归纳两种，一种是针对激活函数的优化，我们依然采用升维-激活函数-降维的结构。而另一种则对整个FFN做结构改造的，比如门控机制以及MOE。

2.2.1 激活函数优化

优化激活的研究，不仅仅局限于FFN，而是整个神经网络。但在FFN的背景下，我们针对激活函数本身研究入手集中在：

神经元死亡问题
更平滑的非线性
激活函数的自适应性
更好的梯度流动

记住这里，后面我们会始终贯穿这些展开。

2.2.2 结构优化

人们不满足于原始FFN的简单“扩展-激活-压缩”结构，探索了更多可能性，比如门控机制、混合专家模型以及FFN深度和广度的探索等等。

3 激活函数的演变

现在我们把时间调回2017年，transformer刚刚提出时，从FFN中最初的激活函数ReLU开始。

3.1 ReLU（Rectified Linear Unit）

ReLU（Rectified Linear Unit） 其简洁高效的计算方式，使其依然是很多研究和开发人员考虑的主要激活函数之一。当输入大于0时，直接输出输入值；当输入小于等于0时，输出0。

3.1.1 公式

R e L U (x) = {\begin{cases} x & 当 x \geq 0 \\ 0 & otherwise \end{cases}

ReLU

3.1.2 ReLU的优点

ReLU的优点可以体现在以下三个方面：

梯度传播方面，ReLU在正区间的导数恒为1，有效避免了传统Sigmoid类函数导致的梯度逐层衰减问题，显著改善了深层网络的训练稳定性；
计算效率方面，ReLU仅需简单的阈值操作（max(0,x)），相比需要指数运算的激活函数，其计算复杂度大幅降低，显著提升了模型训练和推理的速度；
特征表示方面，ReLU的硬饱和特性（负区间输出为0）能够诱导网络产生稀疏激活，这种特性不仅增强了特征的判别性，还通过隐式的正则化作用降低了模型过拟合的风险。这些特性共同构成了ReLU在深度学习中的核心优势，使其成为现代神经网络架构的基础组件之一。

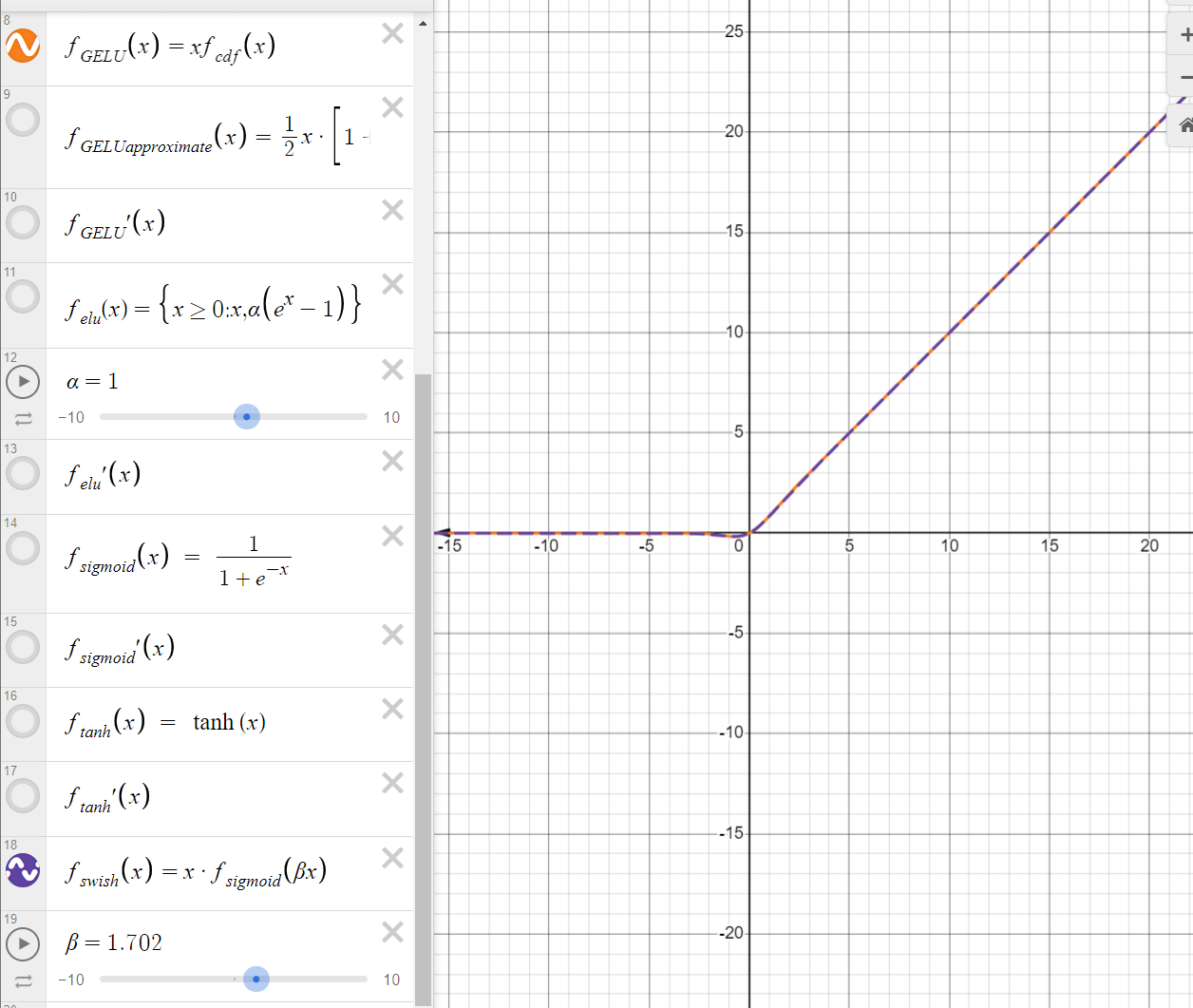
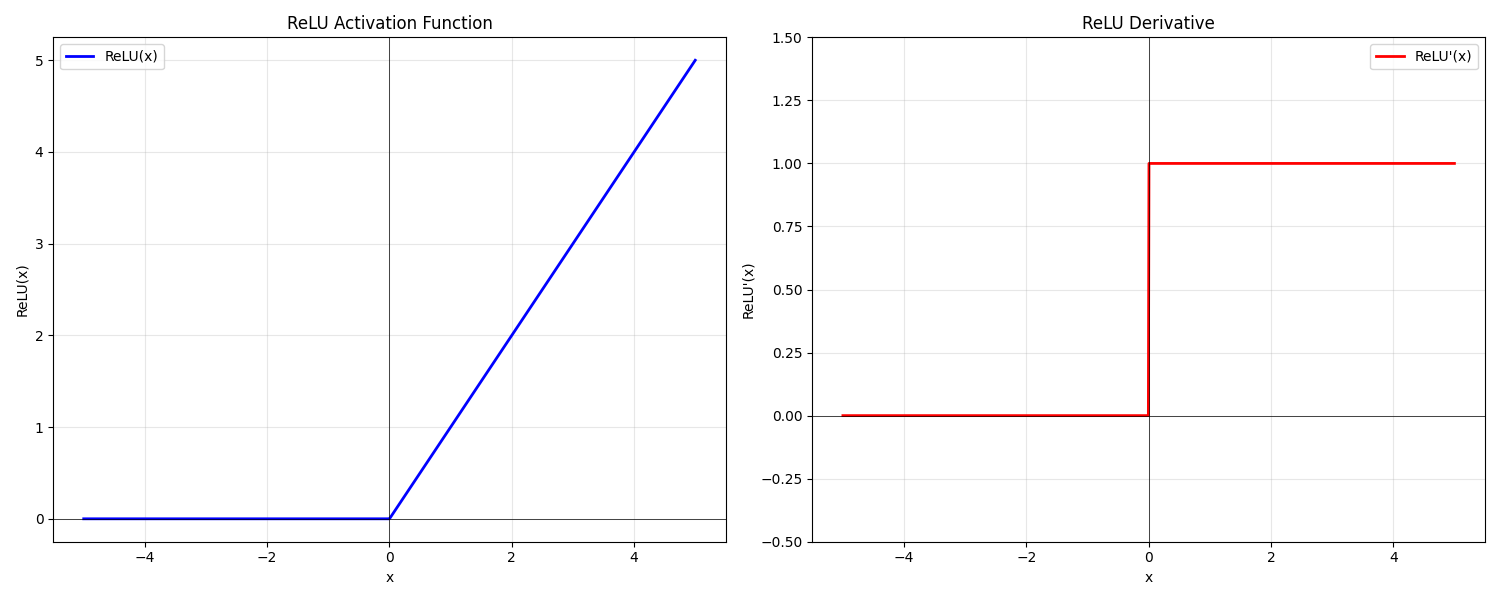
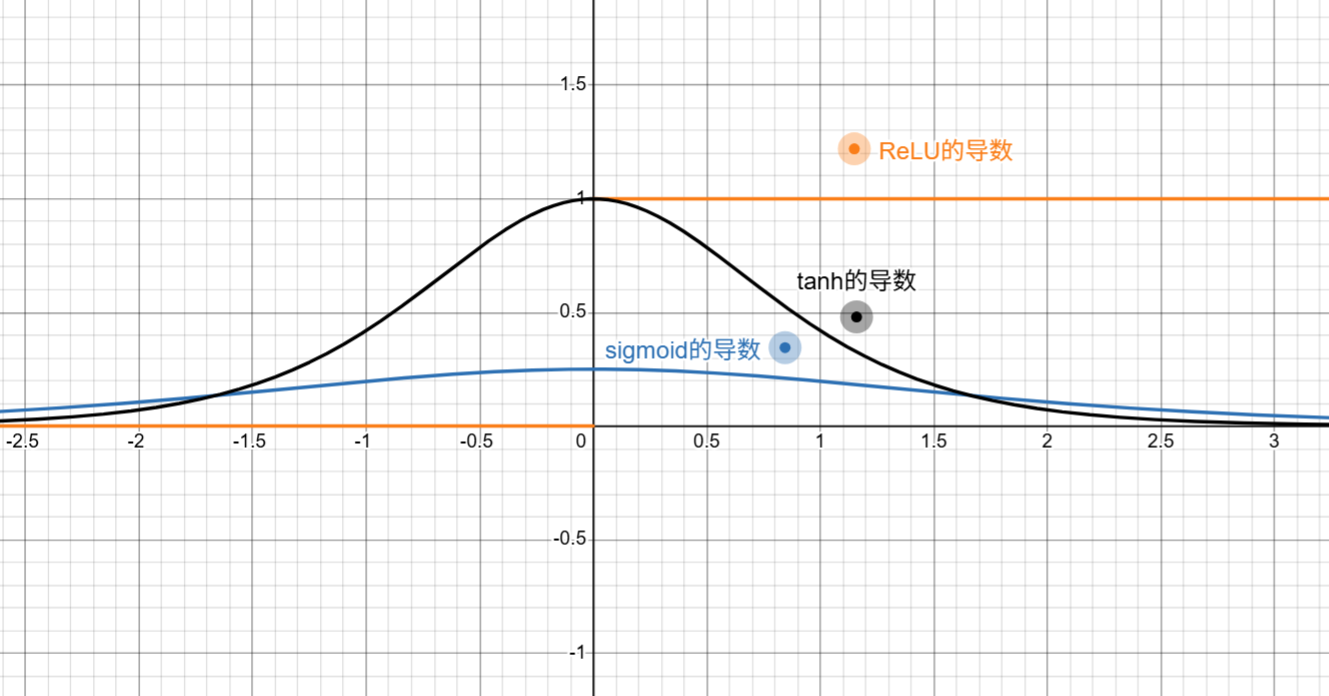
尤其注意的事，ReLU缓解梯度消失问题，主要集中体现在早期S形激活函数（sigmoid和tanh）相比，缓解梯度消失问题。我们可以从这个他们的导数来看。这里比较了三个激活函数的一阶导。ReLU在正区间提供了恒定为1的梯度，只要神经元被激活，那梯度就能无衰减的向前传递。

而tanh和sigmoid则会在输入绝对值较大的情况下无限逼近于0，这就造成了连乘后的梯度指数级衰减，迅速变得非常小。并且sigmoid的一阶导的取值区间在(0, 0.25]所以梯度传递的本身效果就会导致梯度信号会被压缩。

ReLU、tanh、sigmoid导数

3.1.3 ReLU的缺点

然而，ReLU并非完美无缺，其最主要的缺陷是可能导致神经元“死亡” (Dying ReLU) 现象。这种情况通常发生在训练过程中：如果一个ReLU神经元的权重由于某种原因被更新到这样一个状态，使得其对于后续流经的大部分乃至所有训练样本，其接收到的加权输入持续为负值时，那么该神经元的输出将恒定为零。

由于ReLU函数在负区间的导数亦为零，在反向传播计算梯度时，流经该神经元的梯度将因此始终为零。这意味着该神经元的权重参数将无法再通过基于梯度的优化算法进行任何更新。一旦进入这种状态，该神经元在后续的整个学习过程中就永久性地失去了对任何输入做出响应和调整自身参数的能力，仿佛“死亡”一般，无法再对模型的学习做出有效贡献。

如何理解神经元死亡？

举例来说：

我们有这么一个神经元，它受 $w 1$ 、 $w 2$ 以及 $b$ 的影响$$z=w_1 * x_1 + w_2 * x_2 + b$$而ReLU对于这个神经元的值就是$$a = ReLU(z) = max(0, z)$$ 现在，我们假设某一次更新，把 $w_{1} 、 w_{2} 、 b$ 的权重更新成了-0.3，-0.2，和-0.4。并且我们用三组特性不同 $x_{1}$ 和 $x_{2}$

case1： $x_{1} = 2$ 和 $x_{2} = 1$ ，均为正数

z = (- 0.3 * 2) + (- 0.2 * 1) + (- 0.4) = - 1.2

case2： $x_{1} = - 1$ 和 $x_{2} = 3$ 均为负数

z = (- 0.3 * - 1) + (- 0.2 * 3) + (- 0.4) = - 0.7

case3： $x_{1} = 5$ 和 $x_{2} = 5$ 一正一负

z = (- 0.3 * 5) + (- 0.2 * 5) + (- 0.4) = - 2.9

那么以上三种情况，在 $R e L U$ 作为激活函数时，就会导致$$ReLU(z) = 0$$ 多种输入进去以后，都会让 $z$ 的结果为负，从图像上来看，那就是0。可以说一旦陷入这种情况，这个神经元已经无法参与到大部分参数的调整和对模型的贡献上了。

有没有特殊值能救救这个神经元？

确实有一些“特殊值”可以让这个神经元的值 $z$ 为正，但是问题在于，这些特殊值不是大规模的分布在整个输入样本中的（你说他为什么叫特殊值）。所以这个神经元持续地、对大多数样本无法被激活，导致其梯度持续为0，而参数无法更新。如果训练过程中反复的发生这种情况，这个神经元就“死亡”了。

尽管我们说的“永久性”死亡，其实这个永久的实际含义是在当前训练过程和数据分布下，这个神经元无法通过学习自我恢复。即使，我们偶尔遇到一些特殊值有可能让神经元参与一次更新，我们也无法保证这个情况是普遍的，这个神经元在大部分训练时间内不再对模型有积极的贡献了。

如果我改一改激活函数，是不是可以让神经元不死亡？

ReLU在负数区间上恒定为0，导致神经元死亡的问题。所以，如果我给ReLU加上一个斜率，是不是就可以缓解这个问题？

于是你和2013年的论文relu_hybrid_icml2013_final的思想不谋而合。

3.2 Leaky ReLU 和 PReLU（Parametric ReLU）

Leaky ReLU 正是为了解决ReLU的“神经元死亡”问题而诞生的。它的核心思想很简单：当输入小于0时，不再像ReLU那样输出0，而是输出一个很小的、非零的斜率乘以输入值，通常这个斜率α设置为0.01。这意味着即使输入为负，神经元也不会完全“死掉”，仍然允许一个微小的梯度通过，从而避免了神经元“罢工”的现象。

3.2.1 公式

L e a k y R e L U (x) = {\begin{cases} x & if x \geq 0 \\ a x & otherwise \end{cases}

LeakyReLU在不同α值下的图像

同样的，我们从它的一阶导的图来看

尽管Leaky ReLU在一定程度上缓解了神经元死亡问题，但它并非万能药。这个固定的斜率α通常需要手动设置，而且不同的任务可能需要不同的α值，这给模型的调优带来了一定挑战。因此，Leaky ReLU依然存在并非所有任务都适用，以及最佳α值难以确定的问题。

作为Leaky ReLU的扩展，PReLU将负区间的斜率α作为一个可学习的参数，允许模型在训练过程中自适应地学习每个神经元最合适的斜率。这使得PReLU在理论上比固定α的Leaky ReLU更灵活。

P R e L U (x) = {\begin{cases} x & if x \geq 0 \\ a_{i} x & otherwise \end{cases}

那PReLU是不是已经足够好了呢？

显然不是

我们刚刚只是讨论了训练稳定性和计算效率（ReLU系列本身高效的特点）这方面。我们最初的目标说过，优化的方向主要在三个方面。虽然训练稳定性的问题有了一定的提升，那么我们就得开始追求任务的适应性了。

ReLU的另一个特点是单调饱和，也就是当 $x \geq 0$ 时，直接返回 $x$ 。但我们对激活函数还希望它是零均值输出，这可以帮助我们得到更加平滑，更有效率的梯度。如果激活函数的输出是零均值的，那么后续层的权重更新会更加高效，有助于加快学习的收敛速度。

具体来说，如果激活函数的输出总是正的，那么该层权重的所有梯度分量倾向于同时为正或同时为负。这可能导致参数在优化过程中走“之”字形路径，从而减慢了到达最优解的速度。

尽管transformer结构中有normalization或者dropout等其他机制。来调整零均值或者样本分布。它们会一定程度上解决激活函数本身没有的特性，但这里，我们依然针对激活函数本身的优缺点去讨论，而不引入额外的模块去讨论工程上的实现细节。

3.3 ELU

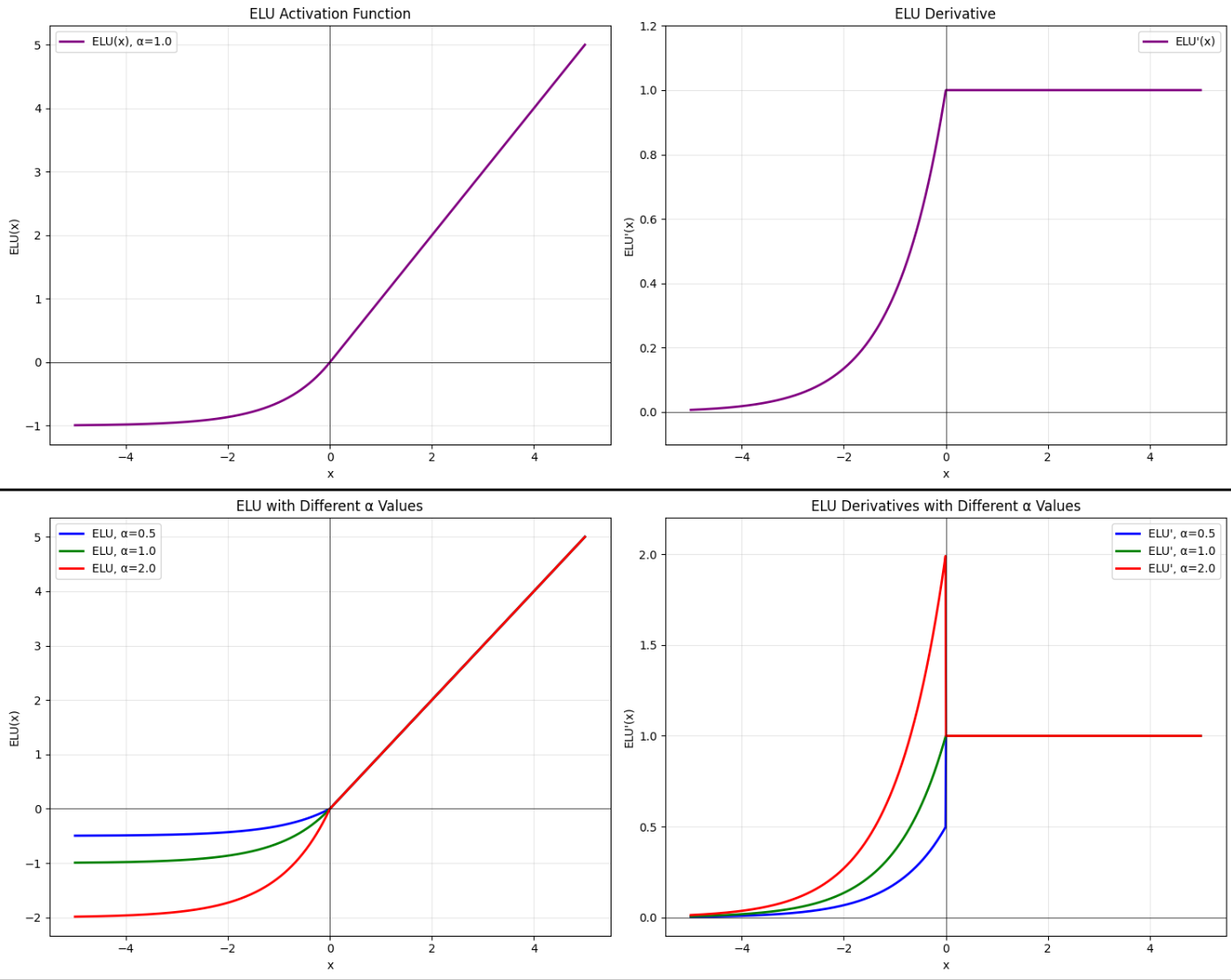
ELU（Exponential Linear Unit） 将ReLU的优点与零均值输出的特性结合起来。当输入大于0时，ELU的行为与ReLU相同；但当输入小于等于0时，它会输出一个平滑的、指数衰减的负值 $α (e^{x} - 1)$ 。ELU的这种设计有两个主要优点：

避免神经元死亡：由于在负值区域有非零输出，ELU彻底解决了ReLU的神经元死亡问题。
输出均值接近零：ELU的负值输出可以帮助网络激活的均值更接近零，这有助于减轻协变量偏移（Covariate Shift） 问题，从而加速学习，并提高训练的稳定性。ELU的平滑特性也有助于减少优化过程中对学习率的敏感度。

3.3.1 公式

ELU (x) = {\begin{cases} x & if x \geq 0 \\ α (e^{x} - 1) & if x < 0 \end{cases}

ELU在不同α值的图像

3.3.2 那么实际情况下真的有那么多人用ELU么？

论文2015年发表的时候，ELU在CIFAR和ImageNet等数据集上，ELU相比ReLU有轻微的性能提升，但提升幅度有限。

因为其理论优势在大规模实践中未能转化为显著的实际收益，同时引入了额外的计算成本和调优复杂度。而且，在工程上有batch norm，相对减少了ELU在的零均值的优势，所以深度学习的组件选择往往是工程权衡的结果，而非单纯的理论最优。

3.4 GELU

但是同样有更高计算开销的GELU却一度成为了transformer推荐的激活函数。这又是为什么？

3.4.1 公式

GELU（Gaussian Error Linear Unit） 其灵感来源于随机正则化器，如Dropout、Batch Normalization。GELU的公式为

GELU (x) = x \cdot P (X \leq x) = x \cdot Φ (x)

其中 $Φ (x)$ 是标准正态分布的累积分布函数（CDF）。简单来说，它将输入值乘以该输入值通过正态分布的“概率”。

GELU (x) = x \cdot Φ (x) = x \cdot \frac{1}{2} [1 + erf (\frac{x}{\sqrt{2}})]

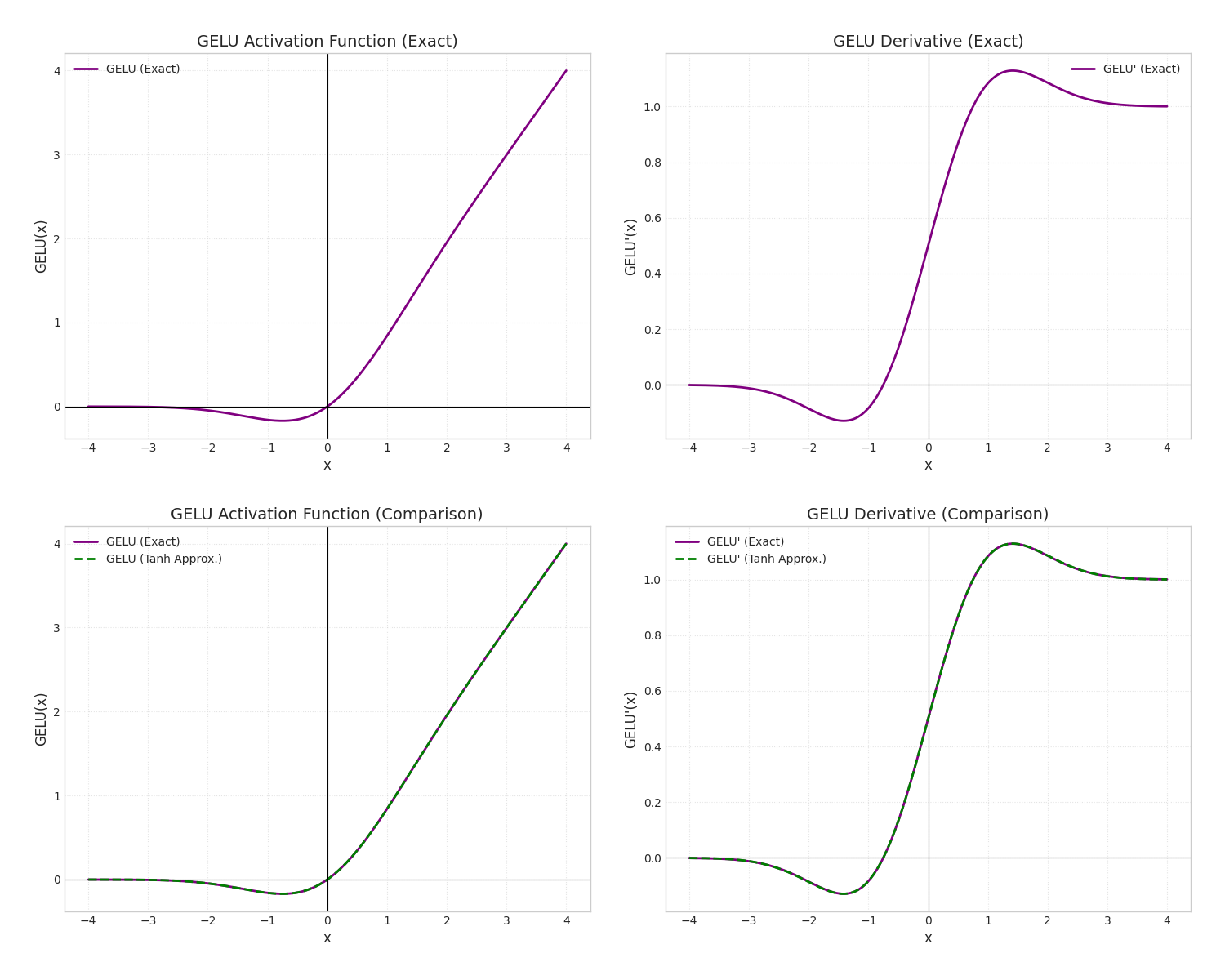GELU及其近似 $Φ (x)$ 的含义: $Φ (x) = P (X \leq x)$ ，其中 $X \sim N (0, 1)$ 属于标准正态分布。它表示一个标准正态随机变量小于或等于 x 的概率。 - 当 $x$ 很大时， $Φ (x)$ 趋近于 1， $G E L U (x) \approx x$ ，类似 ReLU。 - 当 $x$ 很小时 (比如远小于0)， $Φ (x)$ 趋近于 0，GELU(x) ≈ 0。 - 在 $x$ 接近 0 的区域， $Φ (x)$ 平滑地从 0 过渡到 1。

$e r f$ （error function): 也称为也称为高斯误差函数，定义是

erf (x) = \frac{2}{\sqrt{π}} \int_{0}^{x} e^{- t^{2}} d t

这里主要介绍一下 $e r f$ ，知道其公式和计算，不过多展开，在这里它是 $c d f$ 也就是 $ϕ (x)$ 的一部分。而这里的问题在于 $e r f (x)$ 本身没有简单的初等函数解析式，其计算通常需要查表、级数展开或数值积分，这在硬件层面，尤其是GPU和专用AI加速器，上计算成本较高。

$e^{- t ²}$ ：这是标准高斯函数的一部分，表示的是正态分布的钟形曲线，但未归一化且中心在0，标准差为 $1 / \sqrt 2$ 。

$\int ₀ ˣ . . . d t$ ：从0到x对这个高斯函数进行积分，计算曲线下的面积。

$2 / \sqrt π$ ：这是一个归一化常数，使得 erf(∞) = 1 并且 erf(-∞) = -1。

3.4.2 GELU的近似算法

在论文[1606.08415] Gaussian Error Linear Units (GELUs)中，作者就提出了GELU的高效近似算法。这个算法使用tanh去逼近正常的GELU。这个方法好在于许多数学库（如libm, Intel MKL, cuDNN）提供了针对特定硬件指令集的exp和tanh的快速实现，例如通过查表、分段多项式逼近（如泰勒展开或切比雪夫多项式）等方法。这种优化使得tanh的计算远快于直接计算erf函数。尽管是近似，但该方法在实践中被证明能够保持与精确GELU相近的模型性能

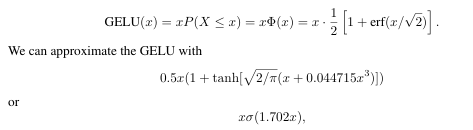Gassian Error Linear Units原文公式

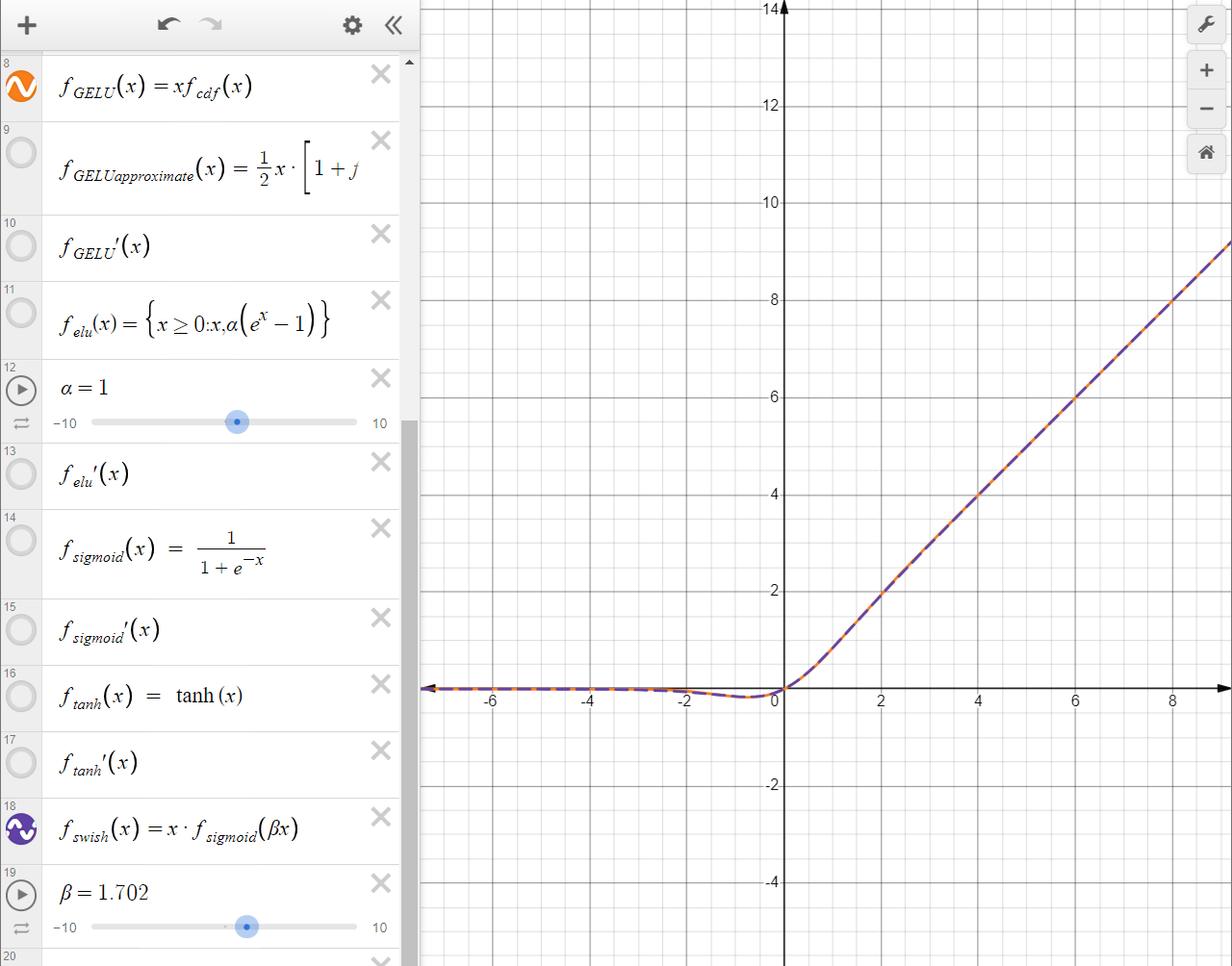
两个GELU图像如下图所示，人眼来看几乎是完全重合了。

GELU与其近似的图像比对

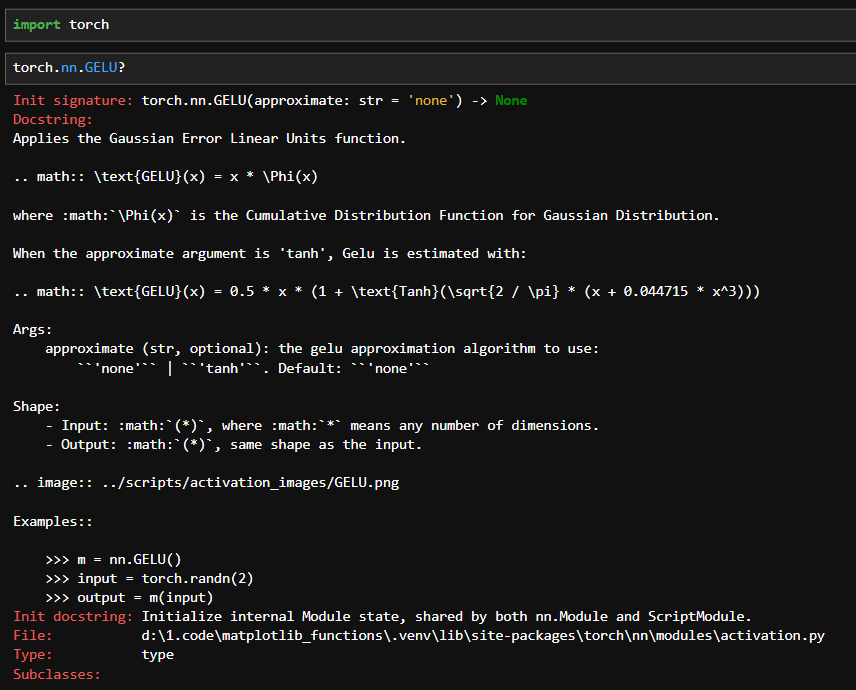
现在我们从代码角度去看，torch.nn.GELU的参数，approximate为true时就会使用这种高效的近似。

torch中的GELU

3.4.3 GELU的优点

对比之前说的几个激活函数。

和ReLU比：
- GELU的整个定义域更为平滑，相比ReLU在x=0这个位置不可导，GELU的平滑特征更为出色突出。
- 避免神经元死亡，GELU对于负输出的导数不恒为0（看上面导数的图）。
- 更强的表达能力，这个其实可以展开说，不过这里就提一个点，在transformer作为大模型的基础架构之后，人们对语言的需求不仅仅是ReLU这种非黑即白。有时候会需要理解一些”隐喻“、”暗讽“以及”阴阳怪气“ 。GELU的曲线更为平滑更能够理解这样的表达。
和LeakyReLU或者PReLU比：
- 依然是更强的表达能力，因为LeakyReLU/PReLU在负值区是线性的，而GELU在负值区是高度非线性的（曲线形状）。
和ELU相比：
- 都是包含了更为复杂的计算，但是GELU展现出压倒性且广泛复现的性能优势，所以GELU成为了transformer中一种推荐的激活函数

3.4.4 搓一个GELU的FFN

python

import torch.nn as nn

class GELUFFN(nn.Module):

    def __init__(self, d_model, d_ff, dropout=0.1):
        super(GELUFFN, self).__init__()
        self.linear1 = nn.Linear(d_model, d_ff)
        self.linear2 = nn.Linear(d_ff, d_model)
        self.dropout = nn.Dropout(dropout)
        
    def forward(self, x):
        x = self.linear1(x)
        x = nn.GELU()
        x = self.dropout(x)
        x = self.linear2(x)
        return x

或者更为简洁的

python

import torch
import torch.nn as nn

class GELUFFNSequential(nn.Module):
    def __init__(self, d_model: int, d_ff: int, dropout: float = 0.1):
        super(GELUFFNSequential, self).__init__()
        self.ffn = nn.Sequential(
            nn.Linear(d_model, d_ff),
            nn.GELU(), 
            nn.Dropout(dropout),
            nn.Linear(d_ff, d_model) 
        )

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        return self.ffn(x)

3.5 Swish/SiLU

Swish也需要提下，因为Swish 函数与 GELU 函数高度接近。从某种意义上说，GELU 可以看作是 Swish 的一个特例或非常近似的变体。但是相比其Swish，GELU在transformer中一度是标配。虽然Swish在某些研究里表现好，但工业界更倾向用GELU。另一个需要提及的原因是后续的门控结构部分，我们需要知道Swish是什么。

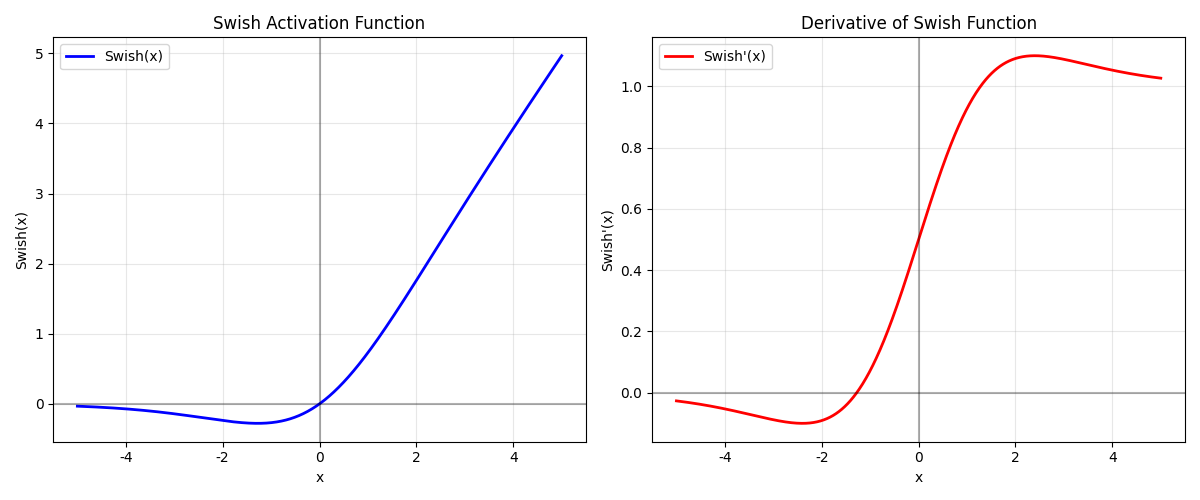
3.5.1 公式

s w i s h (x) = x \cdot σ (β x)

sigma: 就是sigmoid函数
$β$ :是一个可训练的参数，通常默认为1，不过当它为1.702时也是一个特殊值。

Swish及其导数

有没有发现，这个图像居然和GELU高度重合相似。是的，如果我们把 $β$ 设为1.702，就会发现两个几乎重叠的曲线。

Swish的β为1.702时和GELU的比较

所以为什么GELU是transformer中一度推荐的激活函数而Swish不是

GELU论文发表于2016年 ([1606.08415])，而Swish的自动化搜索研究发表于2017年末 ([1710.05941])。当Transformer架构在2017年提出时 ([1706.03762])，GELU已经是当时研究社区探索过并在一些实验中显示出潜力的候选者之一。Transformer的原始论文在比较ReLU和GELU后，选择了GELU作为其默认激活函数。这种“先发优势”使得GELU在Transformer生态建立的早期就被广泛采用。
GELU的理论动机，GELU的设计灵感来源于随机正则化思想，其形式可以被理解为输入根据其自身大小被随机“保留”的期望值，其中“保留”的概率由标准正态分布的累积分布函数决定。这种将输入值与一个依赖于该输入值的概率因子相乘的机制，与Dropout等随机正则化手段有相似的哲学内核，即根据输入信号的强度进行自适应的非线性变换和信息门控。
近似计算，虽然精确计算GELU涉及误差函数（erf），计算成本高于Swish中的Sigmoid，但GELU论文中同时提出了高效的近似算法，例如使用Sigmoid函数或Tanh函数进行逼近。这些近似算法大大降低了GELU的实际计算开销，使其在实践中与Swish的计算成本差距缩小。

当然GELU和Swish也不是激活函数的终点，在这之后还有其他激活函数被发现可用。而且在特定领域下，ReLU等激活函数依然能发挥非常好的效果。单纯从对激活函数的探索来说，理解到为何会有更新的激活函数被挖掘，它们解决了什么问题，从以上内容来说，应该已经足够抛砖引玉。接下来我们要说说对FFN结构改变的一些探索。

4 FFN结构变化

激活函数优化的同时，研究者们也在尝试对FFN结构进行优化。除了现在大家熟知的MOE以外，第一个比较成功结构变化应该是GLU提出的门控结构。

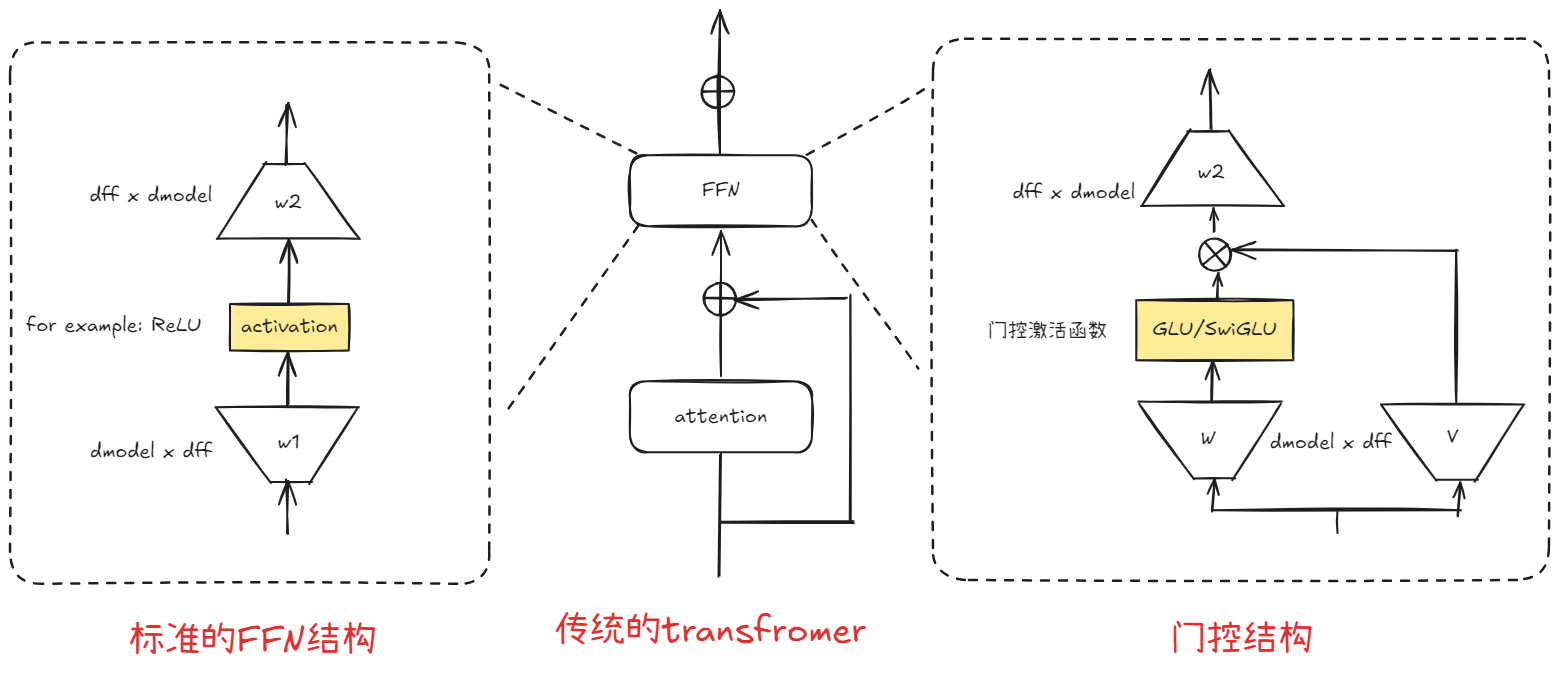
2017年，GLU改变了传统的FFN的升维-非线性-降维的结构。降第一个升维的线性变换和非线性变换整体代替维门控机制。GLU将输入 X 通过两个独立的线性变换成两部分。一部分 (XW + b) 作为主要的待处理信息，另一部分 σ(XV + c) 经过Sigmoid函数后作为门控信号。这个门控信号决定了第一部分信息中哪些元素应该被保留或抑制。如果门控值接近1，则对应的信息通过；如果接近0，则信息被抑制。从下面这张图来看可以看出标准的FFN和门控结构的FFN的区别：

标准FFN和门控结构对比

4.1 GLU/SwiGLU/GeGLU

GLU（Gated Linear Units）的核心思想在于将输入特征线性变换后，一部分直接作为数据通路，另一部分经过Sigmoid函数激活后作为门控信号，两者逐元素相乘得到最终输出。GLU本身是用sigmoid函数作为门控路径。我们可以看做是一种通用结构。

4.1.1 公式

GLU (x) = \underset{主路径}{\underset{⏟}{(W X + b)}} ⊙ \underset{门控路径}{\underset{⏟}{σ (V X + c)}}

X 是输入张量。
W, V 是权重矩阵，b, c 是偏置向量。它们是可学习的参数。
XW + b 通常被称为“数据通路”或“候选激活值”，它对输入进行线性变换。
XV + c 是“门控通路”，也对输入进行线性变换。
σ 是Sigmoid激活函数，其输出范围在 (0, 1) 之间，作为“门控值”。在后续的变体
⊗ 表示逐元素乘法（Hadamard product）。

所以进一步来说我们可以称为这个结构叫做`GLU-Variant(x)·

GLU (x) = \underset{主路径}{\underset{⏟}{(W X + b)}} ⊙ \underset{门控路径}{\underset{⏟}{Activation (V X + c)}}

而其中的差异在于 $A c t i v a t i o n$

Activation \in {σ, GELU, Swish, ReLU \dots}

4.1.2 优点

门控结构的核心优势在于其门控机制，允许网络根据输入动态地过滤或增强信息，而不是像ReLU那样进行静态的阈值判断。这赋予了模型更强的表达能力和灵活性。另一个有点是可以在一定程度上帮助缓解梯度消失问题，因为信息路径并非完全依赖于一个可能饱和或导致梯度为零的单一激活函数。最后，门控结构提供了更丰富的表征，通过两个并行的线性变换和它们的交互，GLU理论上可以学习比单一线性变换加简单激活更复杂的函数。

展开来说，它将输入x分别通过两个独立的线性变换（WX和VX），其中Wx被视为“主要内容”路径，而Vx则经过一个门控激活函数（如Sigmoid）转换为“门控信号”。这种结构的核心优势在于，门控信号会逐元素地调节Wx的内容，使网络能够根据输入特征动态地选择性地放大、衰减或关闭信息通道，实现更丰富的特征交互和条件计算。这种选择性信息流允许模型更灵活地聚焦于与任务最相关的特征组合。虽然主要目的并非解决梯度问题，但这种乘法门控结构理论上也可能提供更平滑的梯度路径或缓解特定激活函数（如ReLU）的硬饱和问题。

在《GLU Variants Improve Transformer》中通过大量实验证明，在多种自然语言处理任务中，采用GLU变体（特别是SwiGLU和GeGLU）的Transformer FFN层，其性能均优于标准的ReLU FFN以及使用单一GELU或Swish激活的FFN。

4.1.3 缺点

尽管GLU带来了显著的进步，但其本身也存在一些可以改进之处，这些不足直接催生了GeGLU和SwiGLU等变体：

Sigmoid门的饱和问题: Sigmoid函数在其输入绝对值较大时容易饱和输出接近0或1，导致梯度消失，这会使得门控机制的学习变得困难，尤其是在深层网络中。如果门控信号长时间饱和在0附近，可能会“杀死”某些神经元或信息通路。
信息损失: 虽然动态选择是优点，但如果Sigmoid门控过于激进地将大量信息置零，可能会导致有价值信息的损失。
候选激活的线性本质: 在原始GLU的定义中，数据通路 (XW + b) 在与门控相乘之前是线性的。这意味着非线性主要来自于Sigmoid门以及后续的逐元素乘法。如果在数据通路也引入一个表现更优的非线性激活函数，可能会带来性能提升。

4.1.4 SwiGLU和GeGLU

因为GLU的这些缺点，所以我们替换掉 $σ$ ，通过Swish和GELU两种激活函数替代公式中的 $σ$ ，从而得到GLU的变体SwiGLU和GeGLU，这两种激活函数均有不错的表现，尤其是对比传统的ReLU、GELU、Swish等，所以大部分人认为在计算性能可接受的情况下，门控机制是一种更为优秀的结构。在原文中提到SwiGLU的分数高达74.56，是平均表现最好的FFN结构。

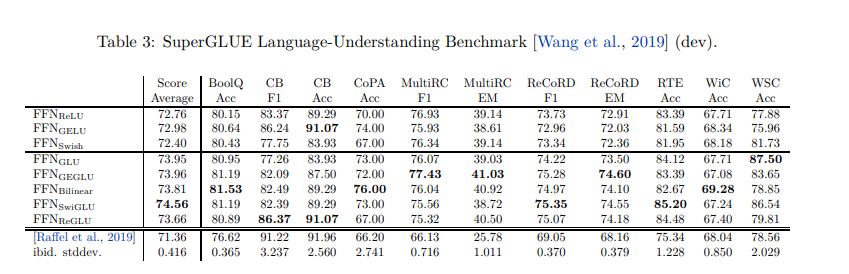GLU vaiants Imporve Transformer原文benchmark对比

那么为什么没有使用门控结构时GELU更为流行，而到了门控结构这里是SwiGLU更优呢？

GELU在早期Transformer FFN层中的流行，源于其理论动机、示范效应、以及独立使用时其近似计算成本尚可接受。然而，当应用于GLU这种对门控函数计算成本极度敏感的结构时，Swish，特别是SiLU, β=1时，展现出了压倒性的效率优势：其核心的Sigmoid门控计算 (σ(x)) 被硬件和软件极度优化，成本远低于GELU所需的误差函数或其近似计算。同时，Swish的结构天然契合门控概念，且在实践中被证明性能优异。

4.1.5 搓一个SwiGLU代码

python

import torch.nn as nn
import torch.nn.functional as F

class SwiGLUFFN(nn.Module):
    def __init__(self, d_model, d_ff):
        super().__init__()
        self.gate_proj = nn.Linear(d_model, d_ff, bias=False)
        self.value_proj = nn.Linear(d_model, d_ff, bias=False)
        self.output_proj = nn.Linear(d_ff, d_model, bias=False)
    
    def forward(self, x):
        gate = F.silu(self.gate_proj(x))
        value = self.value_proj(x)
        return self.output_proj(gate * value)

不过原文中，推荐共享部分参数来减少计算量，具体来说，我们可以用一个大的Linear层代替两个Linear层，然后将其输出拆分为两部分：一部分用于门控，一部分用于值。所以我们可以写成

python

import torch.nn as nn
import torch.nn.functional as F

class SwiGLUFFN(nn.Module):
    def __init__(self, d_model, d_ff):
        super().__init__()
        self.gate_value_proj = nn.Linear(d_model, 2 * d_ff, bias=False)
        self.output_proj = nn.Linear(d_ff, d_model, bias=False)
    
    def forward(self, x):
        combined = self.gate_value_proj(x)
        gate, value = combined.chunk(2, dim=-1)
        return self.output_proj(F.silu(gate) * value)

4.2 MoE

与SwiGLU在激活函数层面通过门控机制动态调整信息流不同，MoE将这种门控思想提升到了模块级别。其核心思想是将一个大的、计算密集的网络层（通常是前馈网络FFN层）替换为多个并行的、规模较小的“专家”子网络，也就是我们称为experts。对于每个输入也就是token表示，一个可学习的“门控网络”或“路由器”会动态地决定将该输入分配给哪个或哪些专家进行处理。

SwigLU可视为MoE的微观基础单元：其门控机制（Swish(xW)）动态调节特征流；MOE将此思想扩展至模型架构层：用门控机制在多个专家间路由，实现计算效率与模型容量的平衡。

由于篇幅限制，而且MoE也是一个需要详细展开的部分，所以这里只能把前面整个从ReLU到门控再到MoE贯穿起来。以后再深入展开。

5 总结

其实激活函数还有很多，比如我们熟悉的 $s i g m o i d$ 、 $t a n h$ ，但是这里都没有提及。我不想非常事无巨细的把每个激活函数都说一遍。主要还是想要通过三个优化目标以及两个优化方向这一框架，说明激活函数到结构变化是如何根据大模型或者其他非语言类任务变化而变化的。

整体来说，我是从ReLU->LeakyRelu/PReLU->GELU/Swish->SwiGLU/GELU->MOE展开的，虽然它们在时间上不是严格的线性递进关系，但背后的优化逻辑是递进的，可以清晰地看出研究者们在提出新的激活函数以及FFN结构时的思考脉络：

激活函数方面：

ReLU崛起，解决梯度消失问题
Leaky ReLU/PReLU出现，解决神经元死亡
ELU尝试零均值输出
GELU/Swish提出基于概率的平滑激活

结构优化方面：

GLU引入门控机制，新的结构被提出
SwiGLU/GeGLU将优秀的激活函数与门控机制结合
MOE：将门控思想扩展到专家网络级别，实现计算效率和模型容量的平衡

最后，这里用到的图分别是matplotlib和desmos。

desmos上关于本篇的激活函数公式在这里：https://www.desmos.com/calculator/k1eaqxrbtn
matplotlib中图像在google colab：https://colab.research.google.com/drive/1ikvg0xVWK872CZbZsbctr6ZL0SXcBqL8?usp=sharing

6 参考

S. R. Dubey, S. K. Singh, B. B. Chaudhuri. (2022). Activation Functions in Deep Learning: A Comprehensive Survey and Benchmark. Neurocomputing. arXiv preprint arXiv:2109.14545. Retrieved from https://arxiv.org/pdf/2109.14545
B. Xu, N. Wang, T. Chen, M. Li. (2015). Empirical Evaluation of Rectified Activations in Convolution Network. arXiv preprint arXiv:1505.00853. Retrieved from https://arxiv.org/pdf/1505.00853
D.-A. Clevert, T. Unterthiner, S. Hochreiter. (2016). Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). Published as a conference paper at ICLR 2016. arXiv preprint arXiv:1511.07289. Retrieved from https://arxiv.org/pdf/1511.07289
TensorFlow Team. (n.d.). tensorflow/playground: Play with neural networks! [GitHub repository]. Retrieved from https://github.com/tensorflow/playground
苏剑林. (2020年3月26日). GELU的两个初等函数近似是怎么来的 [博客文章]. 科学空间|Scientific Spaces. 取自 https://spaces.ac.cn/archives/7309
O. Ozyegen, S. Mohammadjafari, K. El mokhtari, M. Cevik, J. Ethier, A. Basar. (2021). An empirical study on using CNNs for fast radio signal prediction. arXiv preprint arXiv:2006.09245. Retrieved from https://arxiv.org/abs/2006.09245
D. Hendrycks, K. Gimpel. (2023). Gaussian Error Linear Units (GELUs). arXiv preprint arXiv:1606.08415. Retrieved from https://arxiv.org/abs/1606.08415
N. Shazeer. (2020). GLU Variants Improve Transformer. arXiv preprint arXiv:2002.05202. Retrieved from https://arxiv.org/pdf/2002.05202
Y. Tay, M. Dehghani, D. Bahri, D. Metzler. (2022). Efficient Transformers: A Survey. arXiv preprint arXiv:2009.06732. Retrieved from https://arxiv.org/pdf/2009.06732

前馈神经网络（FFN）详解（二）：从激活函数到MOE

作者phimes

发布于2025/6/2

更新于今日内

许可协议 CC BY-NC-SA 4.0

署名-非商业性使用-相同方式共享 4.0 国际

反馈与投诉

前馈神经网络（FFN）详解（二）：从激活函数到MOE

1 前言 ​

2 优化激活函数思路 ​

2.1 优化目标： ​

2.1.1 训练稳定性 ​

2.1.2 计算效率 ​

2.1.3 任务适应性 ​

2.2 优化方向 ​

2.2.1 激活函数优化 ​

2.2.2 结构优化 ​

3 激活函数的演变 ​

3.1 ReLU（Rectified Linear Unit） ​

3.1.1 公式 ​

3.1.2 ReLU的优点 ​

3.1.3 ReLU的缺点 ​

3.2 Leaky ReLU 和 PReLU（Parametric ReLU） ​

3.2.1 公式 ​

3.3 ELU ​

3.3.1 公式 ​

3.3.2 那么实际情况下真的有那么多人用ELU么？ ​

3.4 GELU ​

3.4.1 公式 ​

3.4.2 GELU的近似算法 ​

3.4.3 GELU的优点 ​

3.4.4 搓一个GELU的FFN ​

3.5 Swish/SiLU ​

3.5.1 公式 ​

4 FFN结构变化 ​

4.1 GLU/SwiGLU/GeGLU ​

4.1.1 公式 ​

4.1.2 优点 ​

4.1.3 缺点 ​

4.1.4 SwiGLU和GeGLU ​

4.1.5 搓一个SwiGLU代码 ​

4.2 MoE ​

5 总结 ​

6 参考 ​

1 前言

2 优化激活函数思路

2.1 优化目标：

2.1.1 训练稳定性

2.1.2 计算效率

2.1.3 任务适应性

2.2 优化方向

2.2.1 激活函数优化

2.2.2 结构优化

3 激活函数的演变

3.1 ReLU（Rectified Linear Unit）

3.1.1 公式

3.1.2 ReLU的优点

3.1.3 ReLU的缺点

3.2 Leaky ReLU 和 PReLU（Parametric ReLU）

3.2.1 公式

3.3 ELU

3.3.1 公式

3.3.2 那么实际情况下真的有那么多人用ELU么？

3.4 GELU

3.4.1 公式

3.4.2 GELU的近似算法

3.4.3 GELU的优点

3.4.4 搓一个GELU的FFN

3.5 Swish/SiLU

3.5.1 公式

4 FFN结构变化

4.1 GLU/SwiGLU/GeGLU

4.1.1 公式

4.1.2 优点

4.1.3 缺点

4.1.4 SwiGLU和GeGLU

4.1.5 搓一个SwiGLU代码

4.2 MoE

5 总结

6 参考