1 前言 ​

FFN，也就是前馈神经网络（Feed-Forward Network）是一个相对简单的结构，原版的论文（attention is all you need）里这块描述的比较简洁，直接进入了更深入的部分，虽然叫”attention is all you need" 但是FFN同样重要。对于FFN，我最初的时候也搜了不少资料，依然觉得展开的太少了。所以这次我打算从FFN中的线性和非线性详细展开，当然，这少不了公式和数学的部分，不过我也尽可能的“说人话”。

transformer架构

2 前馈神经网络（FFN） ​

2.1 概念 ​

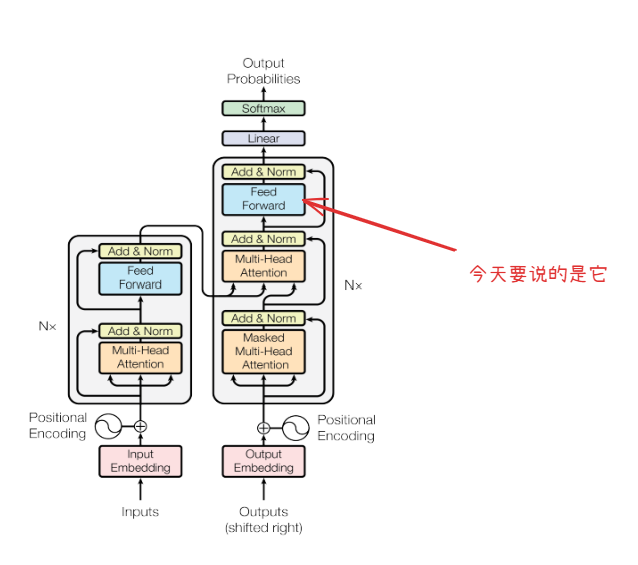
FFN（Feed-Forward Network）作为Transformer架构中的核心组件，本质是一个位置独立的两层感知机。通常FFN位于attention之后，采用"扩展-压缩"维度路径（512→2048→512），通过高维空间中的非线性变换增强表征能力，在高纬空间捕捉更多的信息，然后应用ReLU来提取多的表示，最后再映射回原本的维度。

attention is all you need

FFN

注：图出自 3brown1blue。b站就可以搜到。

2.2 公式 ​

• $x\in R^{d_{model}}$​：输入词向量，比如512维。
• $W_1\in R^{d_{model}\times d_{ff}}$​：第一次线性变换矩阵，扩展维度，比如512×2048。
• $W_2\in R^{d_{ff}\times d_{model}}$​：第二次线性变换矩阵，还原维度，比如2048×512。
• $Activation$：如$ReLU$或$GELU$，提供非线性。

2.3 代码 ​

手搓一个FFN也非常简单

import torch
import torch.nn as nn

class PositionWiseFFN(nn.Module):
    def __init__(self, d_model=512, d_ff=2048, activation=nn.ReLU()):
        super().__init__()
        self.linear1 = nn.Linear(d_model, d_ff)
        self.activation = activation
        self.linear2 = nn.Linear(d_ff, d_model)
        
    def forward(self, x):
        x = self.linear1(x)
        x = self.activation(x)
        x = self.linear2(x)
        return x

ffn = PositionWiseFFN(d_model=512, d_ff=2048)
input_tensor = torch.randn(2, 10, 512)
output = ffn(input_tensor)

3 线性和非线性 ​

这里我们要搞清楚这个问题，我们得先说说线性变换的特点。

3.1 线性 ​

从数学角度看，线性函数的核心思想可以表示为输入特征的加权和，例如一维形式 $y=wx+b$。在更高的维度上通常表示为矩阵乘法加上一个偏置向量

常见的线性变换操作包括拉伸/缩放 (Scaling)、旋转 (Rotation)等。这些操作不会改变空间的“线性”本质。

我们简化一下情况，我们有一个二维的特征空间，比如我们用两个特征来描述一个动物，以一个二维特征空间为例，假设用以下两个特征来描述一个动物：

• $x1$​: 体重 (kg)
• $x2$: 奔跑速度 (km/h)

我们的“猫”和“狗”在这个空间中是两个点 $\mathrm{猫}：C=\left(\begin{array}{c}x1c\\ x2c\end{array}\right)$ ，如果猫的特征向量为$\left(\begin{array}{c}5\\ 40\end{array}\right)$，那其显示意义则表示体重5kg，奔跑速度40km/h。

3.1.1 线性操作 ​

3.1.1.1 拉伸 ​

现在我们的二维的变换矩阵$W_{stretch}=\left(\begin{array}{cc}a& 0\\ 0& b\end{array}\right)$，其中：

• $a$是对特征$x_1$ （体重）的缩放因子。若$a>1$ ，则拉伸；若$0<a<1$ ，则压缩。
• $b$是对特征$x_2$ （奔跑速度）的缩放因子，含义类似。

使用缩放矩阵$\left(\begin{array}{cc}1& 0\\ 0& 2\end{array}\right)$对猫的特征进行变换：

我们线性变换的第一个特征没有任何变化，但是第二个特征翻倍了。

3.1.1.2 旋转 ​

一个通用的二维旋转矩阵（绕原点逆时针旋转 角）$W_{rotate}=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)$如果我们要逆时针旋转90°，那就是$W_{rotate\mathrm{\_}90}=\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right)$，当$X_{cat}$旋转后可以得到： $W_{rotate\mathrm{\_}90}·X_{cat}=\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right)\left(\begin{array}{c}5\\ 40\end{array}\right)=\left(\begin{array}{c}-40\\ 5\end{array}\right)$

让我们先忽略其实际意义，-40kg的猫不存在在这世界上，仅仅关注数学上的效果。

3.1.2 特点和局限性 ​

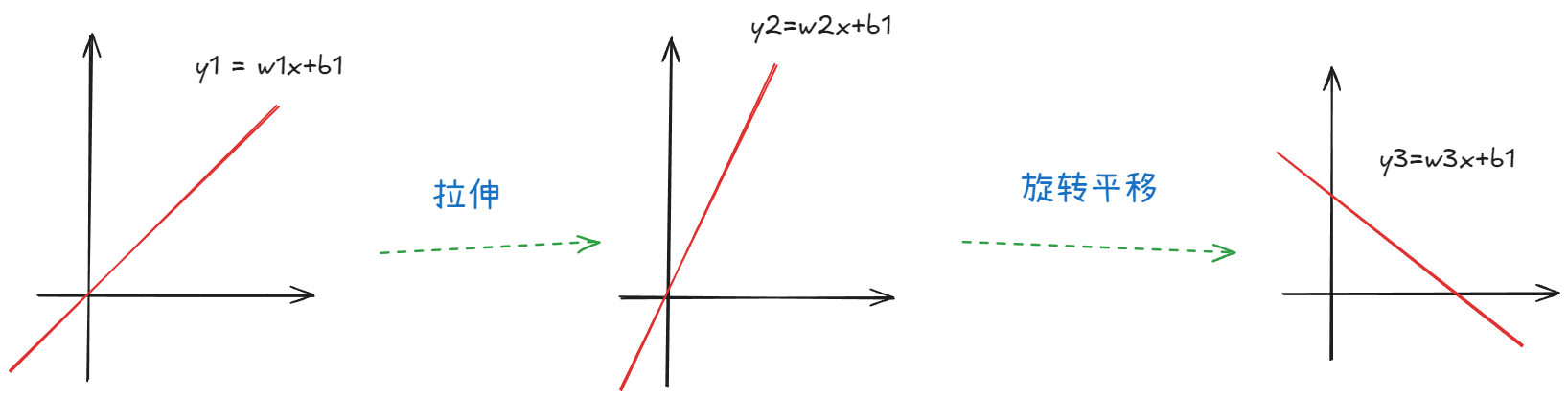
这是一个二维线性方程，我们可以对它做任何线性符合变换，比如拉伸，和平移旋转。

多次线性变换

3.1.2.1 线性特征不变 ​

我们可以得到第一个核心结论：如果我们对直线施加多少次不同的线性变换，其结果在几何上仍然会是一条直线或超平面。它们无法从根本上增加数据的复杂性或引入非线性关系。

这句话怎么理解呢？

意思就是，如果我们想设定一个标准，比如定义“某个速度值以上算作快，以下算作慢”，并以此对动物进行分类，单纯的线性变换是无法直接实现这种基于阈值的非线性决策边界的。 线性变换无法将原始的线性空间 “弯曲”或“折叠” 来区分出这样的“快慢”区域。

即使放到更高维的空间也一样，我们对特征，猫和狗的速度，进行多次线性缩放或旋转，我们也只是在现有的特征维度上进行调整。我们可以通过线性变换放大或缩小速度这个特征值，以便更好地比较，但是我们依然无法找到一个位置、范围明确的说”这猫跑的也太快了！“

显然终于能说这个词了，因为线性的特点，我们无法用一条直线或一个超平面去解决XOR逻辑这类问题，想要解决这类问题就需要引入非线性变换或更复杂的模型结构。

3.1.2.2 多次线性变换等效于一次 ​

第二个核心结论是：多个线性变换的复合（矩阵乘法）等效于一个单一的线性变换，也就是$W_2(W_{1}X)=(W_2{W}_1)X$，最终等效于一次变换 $WX$

让我们回顾一下FFN公式

如果我们没有$Activation$这个激活函数，那我们的$FFN$的两次线性变换就相当于上面的$W_2(W_{1}X)=(W_2{W}_1)X$，这两次线性变换实际就退化成了一层

结合特点一，单一的线性层实际上没有扩展模型的表达能力。于是我们就必须要有一个非线性函数才可能扩展模型的表达能力。

3.2 非线性 ​

非线性函数没有固定的通用形式，但在神经网络中通常指的是激活函数，常见ReLU, GELU等。在原版的，朴素的Transformer中，这个激活函数是ReLU。那么我们的FFN就是

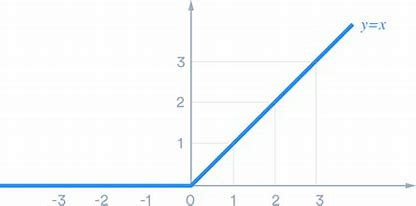
而$ReLU$又是一个非常简单明了的公式：$ReLU(x)=max(0,x)$

ReLU

其原理十分直观：当输入值$x$小于0时，其对应的特征将被抑制为0；而当$x$大于或等于0时，则直接返回该特征值。

这种非线性对线性而言，就可以提取出更多含义，之前说的，如果我们一定要找一个值规定快和慢的话，我们就可以使用ReLU有效地实现这种“开关”或筛选功能。

3.2.1 例子 ​

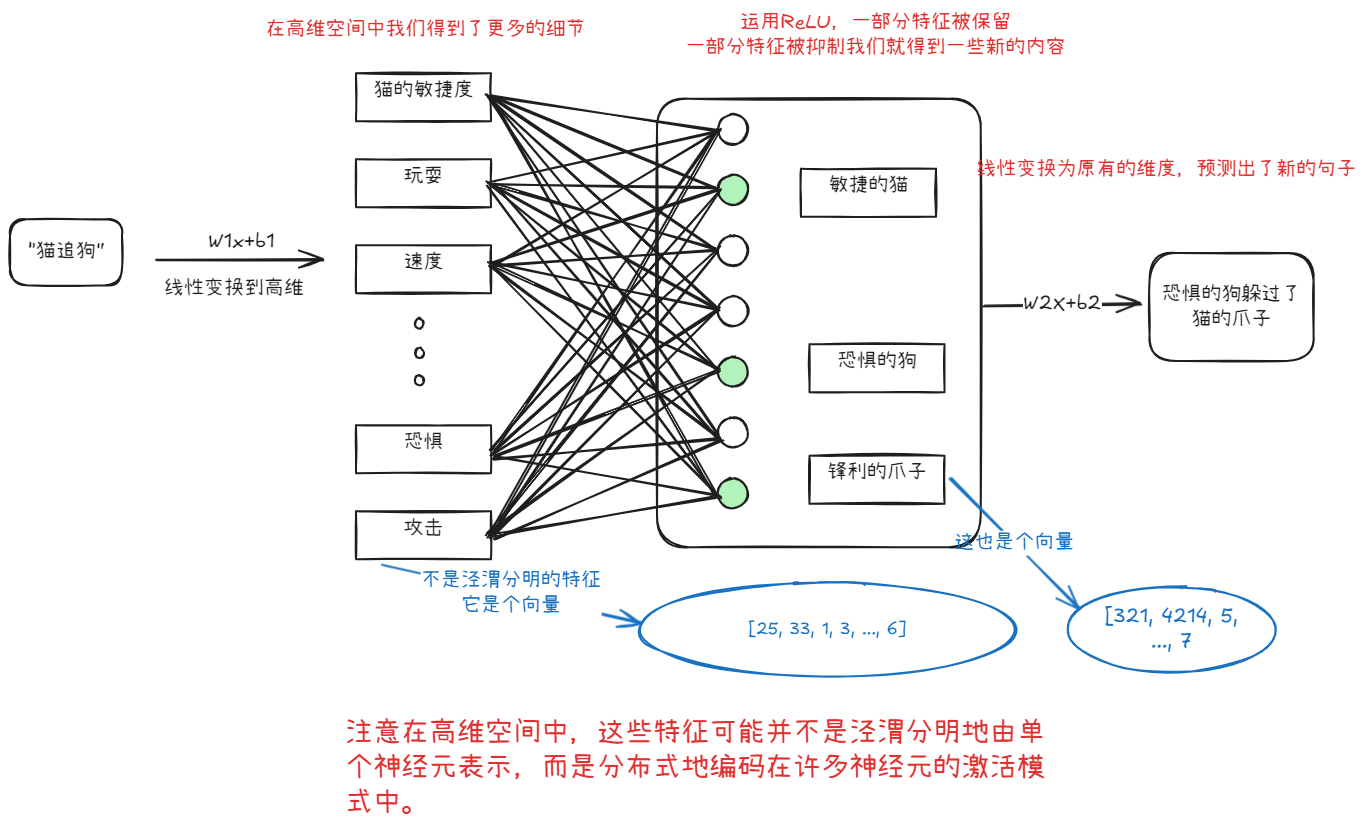
当我们使用激活函数，其非线性特征，ReLU帮助模型关注当前输入下真正重要的特征组合。它允许模型学习非线性的决策边界。比如，只有当“猫的敏捷性”特征、“追逐的快速移动”特征和“狗的逃跑姿态”特征同时达到一定强度时，模型才会将它们组合起来，形成一个更强烈的“猫成功追逐狗”的判断。

在高维空间中，这些特征可能并不是泾渭分明地由单个神经元表示，而是分布式地编码在许多神经元的激活模式中。一个神经元的激活可能同时贡献于多个细微特征的表达。

FFN的线性和非线性可视化对比-使用非线性

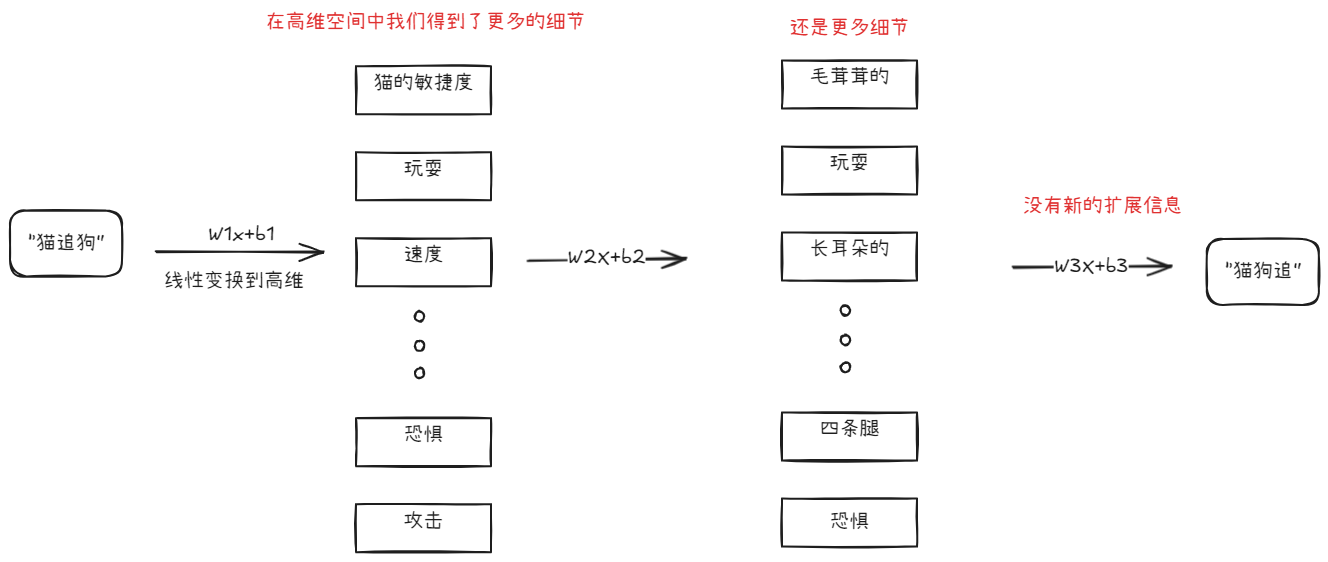
假设，我们没有使用非线性函数会怎样，我们在高维空间中得到了更多的细节，然后不断的应用线性变换，这些细节被展开又被压缩。但是他们依然只是这些细节，没有新的有效信息。最终即使组成了新的句子，也可能是毫无含义的内容，因为对于模型而言，很多信息没并没有被组合。

FFN的线性和非线性可视化对比-只使用线性

到这里，我们终于说完了线性和非线性的特点。这里也就是为什么我们的transformer中必须要有FFN，而FFN中又必须要又非线性的激活函数。

4 其他问题 ​

这是从实际设计角度出发，Attention机制的核心功能是建模token之间的依赖关系，并进行信息聚合。它允许模型中的每个token关注输入序列中的所有其他token，并根据相关性权重来融合这些token的信息，从而生成一个上下文感知的token表示。这时，每个token的向量已经融入了来自序列中其他token的上下文信息。

FFN层对每个token的表示进行独立的、更深层次的变换。它的目标是进一步处理和提炼Attention层输出的、已经包含了上下文信息的特征，增强模型的表达能力。可以理解为，Attention负责“混合”信息，FFN负责对混合后的信息进行“精炼”和“转换”

如果顺序颠倒，FFN在注意力之前处理token，那么它只能对孤立的、缺乏上下文的token信息进行加工，这会限制其学习到与语境相关的复杂特征，而后续的注意力层也只能在这些相对初级表征的基础上进行信息交互，可能会削弱整体模型的性能。

当然，我们并不是说这就是绝对最优的选择，有一些研究探索将Attention和FFN或其变体并行处理以尝试获得更好的效果。但是就目前来说，先于attention的FFN并没有成为主流。

还记得注意力的公式么？

最主要的一个理由是注意力输出的本质是线性组合：尽管softmax在计算注意力权重时引入了非线性，但注意力层的输出实际上是值向量（Value）的加权求和，即使权重是非线性的，最终的聚合操作仍是线性的。

这两个问题放一起，主要是他们的回答比较相似。FFN本身就是一个MLP，中间有多少个隐藏层确实是可以改变的。但是很多时候我们要从功利角度去考虑，即效率和简洁。所以我们确实可以增加隐藏层数量，进行多次的线性变换，也可以使用更高的维度。但更多时候，通过实验，我们更想在效果足够好的情况下，使用更少的资源，更好的效率。

要知道attention is all you need，也就是transformer是2017年提出的。

虽然，一些研究和理论，也会随着性能提升而改变，所以在当时，来自google的研究者们只是做了当下最好的选择。

篇幅限制，将来会说到。

参考 ​

• 3Blue1Brown. (2025，2月，23日）. 【官方双语】大语言模型的简要解释 [视频]. 哔哩哔哩. Retrieved from https://www.bilibili.com/video/BV1xmA2eMEFF/
• Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., & Polosukhin, I. (2017). Attention is all you need. In Advances in neural information processing systems 30 (NIPS 2017) (pp. 5998-6008). Curran Associates, Inc.
• 张俊林. (2020, 11月 24日). 探秘Transformer系列之（十三）--- Feed-Forward Networks. 知乎专栏. Retrieved from https://zhuanlan.zhihu.com/p/29534701208
• Zhao, W. X., Zhou, K., Li, J., Tang, T., Wang, X., Chen, Y., Yin, D., Yu, J., Wang, S., Ma, C. L., Du, X., Liu, Y., Zhang, X., Dong, Z., Gong, Y., He, P., Wen, J.-R., Chen, Z., Zhang, P., ... Yan, R. (2023). A survey of large language models. arXiv preprint arXiv:2305.13297. Retrieved from https://arxiv.org/abs/2305.13297