写在前面
如果对注意力机制本身不太理解的,建议先看从Q和K理解Transformer的注意力机制。然后再来看这篇。
注意力机制
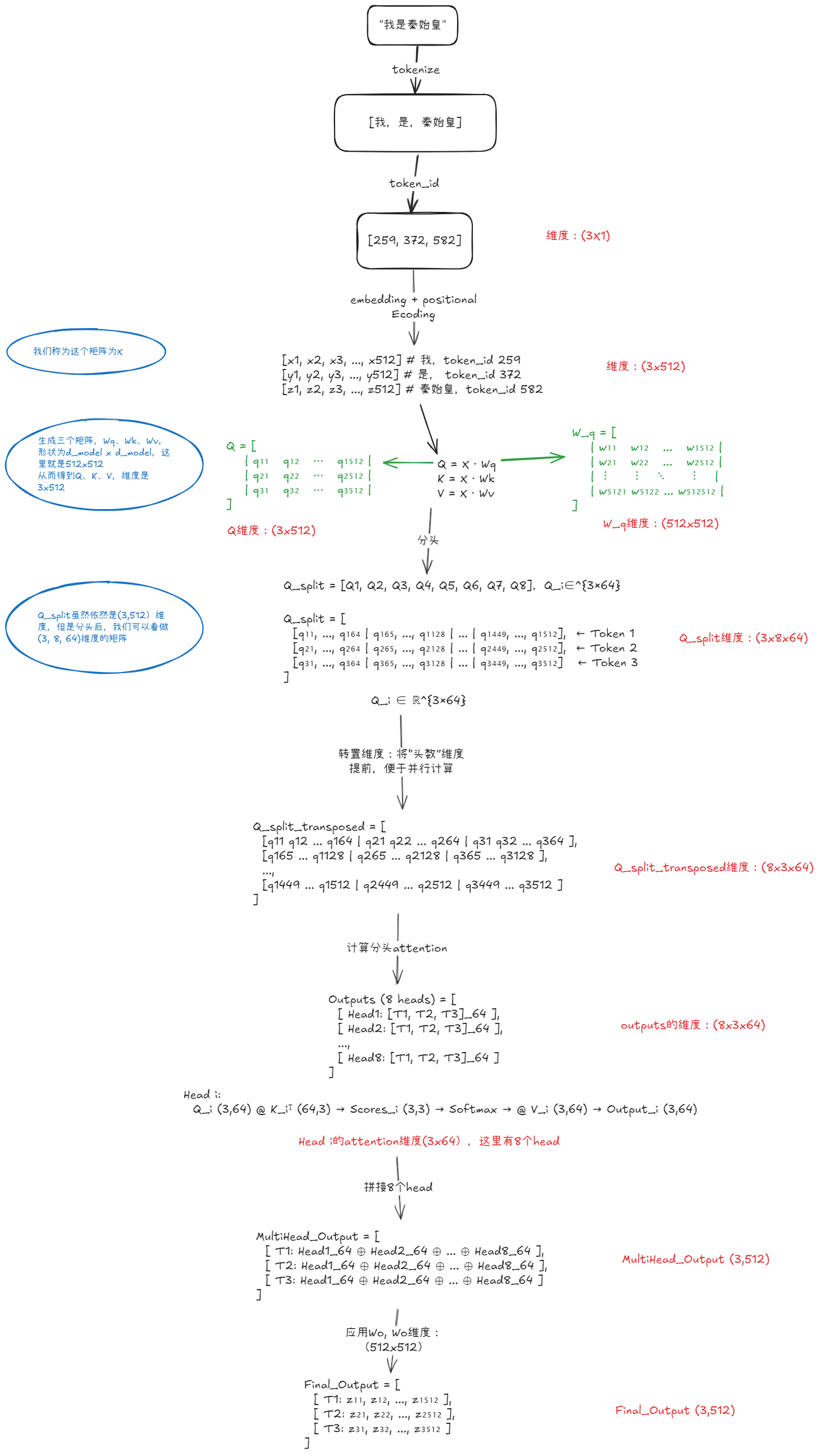
首先简单回顾一下transformer的流程。我们有一句话我是秦始皇。这个内容会首先进行token分词,然后映射为token id,接着我们会对token_id进行词嵌入,得到然后加入位置编码,得到X。整个步骤如下:
- Tokenization:将句子分割成token,
["我", "是", "秦始皇"]。 - Token to ID:将token映射为数字ID,
[259, 372, 5892]。 - Embedding:将ID通过嵌入层转换为向量,
shape=[3, d_model]的矩阵)。这里d_model是模型的维度,一般也就是一个token在高维空间的表示,一般我们用512。 - 位置编码:为每个向量添加位置信息,得到最终的输入表示
X。
不过我们的输入不一定是一个,所以整个输入的就(batch_zise, seq_len, d_model)。其中:
batch_size就是一次输入几个。seq_len就是句子长度。d_model为当前模型的维度。
现在得到输入形状 :(batch_size,seq_len,dmodel),例如 (1,5,512)。
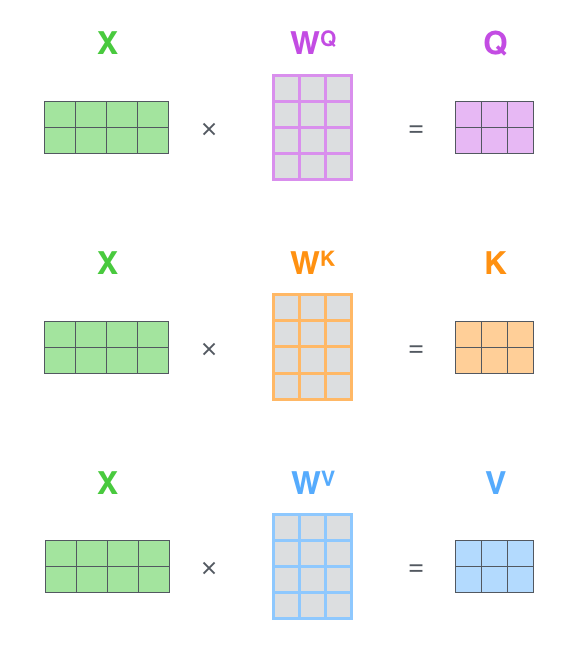
接着应用注意力机制,生成随机的权重矩阵
接着计算注意力得到:
这里就是单头注意力。
多头注意力机制
多头注意力,可以直接理解为我们有多个脑袋去注意不同的事情,从全局角度来看,更为全面。那么怎么做到呢?
通过将Q/K/V投影到不同的子空间(subspace),使模型能够并行学习多种语义特征。具体实现分为四个步骤:
- 有三组权重矩阵
, , 是头的数量 - 分别计算每个头的
- 每个头独立计算注意力
, - 通过
投影回原空间
最终我们将所有的头输出进行拼接得到
代码实现
import torch
import torch.nn as nn
import torch.nn.functional as F
class MultiHeadAttention(nn.Module):
def __init__(self, d_model, num_heads):
super(MultiHeadAttention, self).__init__()
assert d_model % num_heads == 0, "d_model must be divisible by num_heads"
self.d_model = d_model
self.num_heads = num_heads
self.head_dim = d_model // num_heads
self.W_q = nn.Linear(d_model, d_model)
self.W_k = nn.Linear(d_model, d_model)
self.W_v = nn.Linear(d_model, d_model)
self.W_o = nn.Linear(d_model, d_model)
def split_heads(self, x):
batch_size, seq_len, _ = x.size()
x = x.view(batch_size, seq_len, self.num_heads, self.head_dim)
return x.transpose(1, 2)
def scaled_dot_product_attention(self, Q, K, V, mask=None):
scores = torch.matmul(Q, K.transpose(-2, -1))
scores = scores / torch.sqrt(torch.tensor(self.head_dim, dtype=torch.float32))
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
attention_weights = F.softmax(scores, dim=-1)
output = torch.matmul(attention_weights, V)
return output, attention_weights
def forward(self, query, key, value, mask=None):
"""
前向传播过程
query/key/value: 输入张量,形状均为(batch_size, seq_len, d_model)
mask: 可选的掩码张量
返回:输出张量和注意力权重
"""
# 重点关注forward里和理论不同的部分
# 1. 线性变换生成Q/K/V
Q = self.W_q(query) # (batch_size, seq_len, d_model)
K = self.W_k(key)
V = self.W_v(value)
# 2. 分割为多个头的表示
Q = self.split_heads(Q) # (batch_size, num_heads, seq_len, head_dim)
K = self.split_heads(K)
V = self.split_heads(V)
# 3. 计算多头注意力
attention_output, attention_weights = self.scaled_dot_product_attention(Q, K, V, mask)
# 4. 合并多个头的输出
# 先转置回(batch_size, seq_len, num_heads, head_dim)
attention_output = attention_output.transpose(1, 2)
# 合并最后一个维度(num_heads * head_dim = d_model)
batch_size, seq_len, _, _ = attention_output.size()
concat_output = attention_output.contiguous().view(batch_size, seq_len, self.d_model)
# 5. 最终的线性变换(W_o)
output = self.W_o(concat_output) # (batch_size, seq_len, d_model)
return output, attention_weights
if __name__ == "__main__":
batch_size = 2
seq_len = 10
d_model = 512
num_heads = 8
query = torch.randn(batch_size, seq_len, d_model)
key = torch.randn(batch_size, seq_len, d_model)
value = torch.randn(batch_size, seq_len, d_model)
mha = MultiHeadAttention(d_model=d_model, num_heads=num_heads)
output, attn_weights = mha(query, key, value)
print("输入形状:", query.shape)
print("输出形状:", output.shape)
print("注意力权重形状:", attn_weights.shape)问题
为什么多头可以代表多种子语义?
在训练过程中,不同注意力头的参数矩阵(
)会接收到不同的梯度信号,迫使它们沿着不同的方向更新参数,最终学习到不同的特征模式。这种分化是优化过程的必然结果
其关键机制在于:
- 参数独立,参数矩阵
在初始化的时候是随机,不同的 ,扔骰子的时候,多半也是不太相同的。(当然也可能很接近,不过我们还有其他机制) - 梯度多样性,损失函数
多头情况下,每个
- 注意力权重计算的非线性性。因为注意力公式中的
的指数运算而放大特定部分,而其他位置会被抑制,所以每个头的梯度方向自然也就不同了。$$head_i = \text{Attention}(Q^i,K^i,V^i) = softmax(Q^iK^iT/\sqrt{ d_{k} })V^i$$ - 损失函数的隐式正则化,假设我们有2个或者2个以上的头的梯度方向高度一致,那么参数的更新也就趋向一致,那么这就存在
梯度消失这一现象,为了避免这一现象。损失函数会尽可能的让他们的梯度不同。 - 头之间的正交性,对于多个头在训练过程中,如果他们的梯度不同,更新方向不同,且训练有效,那么头的参数矩阵会逐渐展现出正交性。这说明他们在不同语义子空间上学习的不同。
总结下来可以归纳出重要的三点:参数独立、注意力权重的非线性计算、损失函数的特点共同造成训练过程中头之间的差异性。
假设我们有两个头,分别称为
:学习到局部的关系,比如“尊贵的X1车主” :学习到长程的关系,比如”他最喜欢的车是保时捷,但准备买的是X5,最终妥协买了X1“
这里X5和X1都指的是车,它除了实体的识别外,还需要对”车“这个词的长程依赖。所以损失函数
这就直接导致了,在反向传播时,
头的数量是如何选定的?
结论上来说,头的数量选定是计算效率、特征多样性以及维度分配的结果。通常是经过多次试验验证结果。常见的模型的头数量如下:
- transformer: 8头,每个头64维,总维度512
- BERT-base: 12头,每个头64维,总维度768
- BERT-large:16头,每个头64维,总维度1024
- GPT-3 175B:96头,每个头128维,总维度12288
头数量分配原则
- 每个头的维度需要足够大以捕获有效信息,从过往经验来看通常是≥64维
- 经验性调优:测试不同的头在不同任务下效果,选择性能最佳。
- 计算效率:头数量增加可以提升模型的并行性。
输入的维度是如何变化的
最后
- 头的数量可以动态调整么?
- 如果训练时发现头之间存在冗余的情况,是否可以主动调整参数?